Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

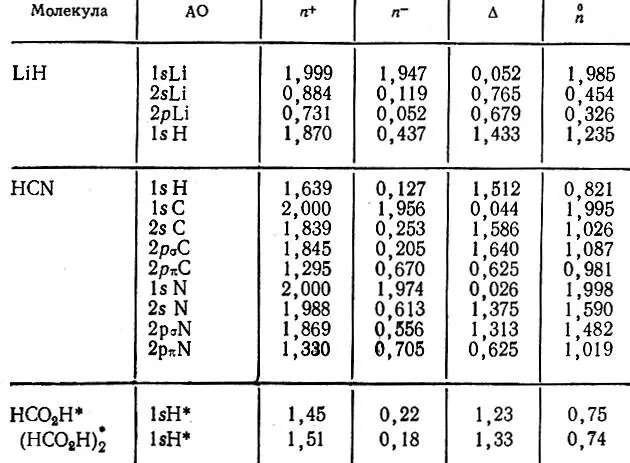
Таблица 10. Анализ заселенностей АО в молекулах LiH, HCN, НСO 2Н, (НСO 2Н) 2

4. Анализ заселенностей АО в молекуле HCN (см. табл. 10) свидетельствует о том, что АО π-типа характеризуется существенно меньшими по сравнению с АО σ-типа значениями заселенностей перекрывания. Малые значения формальных атомных зарядов в HCN указывают на ковалентный характер химической связи в этой молекуле.

5. Анализ заселенностей атомов водорода, ответственных за образование водородной связи, в молекулах муравьиной кислоты и ее димера (см. табл. 10), осуществленный на основе расчета матрицы плотности расширенным методом Хюккеля с самосогласованием по формальным зарядам атомов, показывает, что водородная связь обусловливает заметное изменение электронных заселенностей мостикового атома водорода (Н *). При этом заселенность перекрывания существенно возрастает вследствие увеличения полной и уменьшения неподеленной заселенностей. В то же время аддитивная заселенность и соответствующий ей формальный заряд атома водорода почти не изменяются.

Анализ заселенностей по Малликену.Наряду с изложенным выше подходом к анализу заселенностей существуют альтернативные подходы к этой проблеме. Наиболее популярными до настоящего времени являются предложенные Малликеном [67] определения нетто-заселенности Р аа, заселенности перекрывания

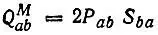(4.80)

и полной зеселенности

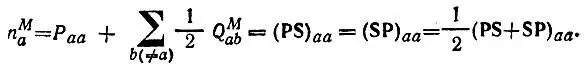(4.81)

В основе этих определений фактически лежит равенство

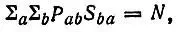(4.82)

представляющее условие нормировки матрицы плотности на число электронов (N) в молекуле. Левую часть этого равенства можно записать в виде суммы членов, относящихся к отдельным АО и их парам:

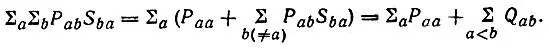(4.83)

Таким образом, сумма нетто-заселен ноет ей всех АО и всех заселенностей перекрывания оказывается равной числу электронов в системе.

Однако это нельзя рассматривать как обоснование анализа заселенностей по Малликену ввиду неоднозначности разложения вида

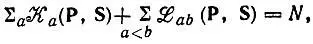(4.84)

где слагаемые 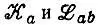выражены через элементы матрицы плотности Р аbи интегралы перекрывания S ab.

Серьезным аргументом против предложенного Малликеном анализа заселенностей является то, что нетто- и полные заселенности могут принимать значения Р aa>2 и n M a>2. Не меньшую трудность представляет интерпретация отрицательных значений Q M ab , имеющих смысл отрицательного числа электронов, приходящихся на связь АО φ aи φ b.

Анализ заселенностей по Христоферзену и Бэкеру[33] формулируется в терминах коэффициентов разложения МО ψ iпо базисным АО φ a:

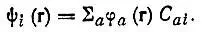(4.85)

При этом предполагается, что вес (или заселенность) АО φ a, входящей в состав МО ψ i, пропорционален квадрату модуля соответствующего коэффициента φ a:

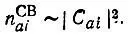(4.86)

Из условия нормировки

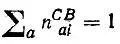(4.87)

для 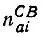получается выражение

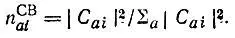(4.88)

Суммированием величин n aiпо всем МО ψ iс учетом их заселенностей далее определяются величины

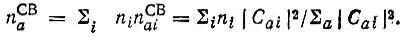(4.89)

Заселенности АО по Христоферзену и Бэкеру, как и заселенности по Малликену, могут принимать значения n CB a>2 (табл 11). В связи с этим интересно отметить, что Христоферзен и Бэкер обращали внимание на недопустимость таких значений, когда речь шла о малликеновском анализе заселенностей. Не менее серьезным обстоятельством, компрометирующим определение Христоферзена и Бэкера, является его неинвариантность относительно унитарного преобразования занятых МО, в то время как одноэлектронная матрица плотности и математические ожидания всех физических величин инвариантны относительно такого преобразования.

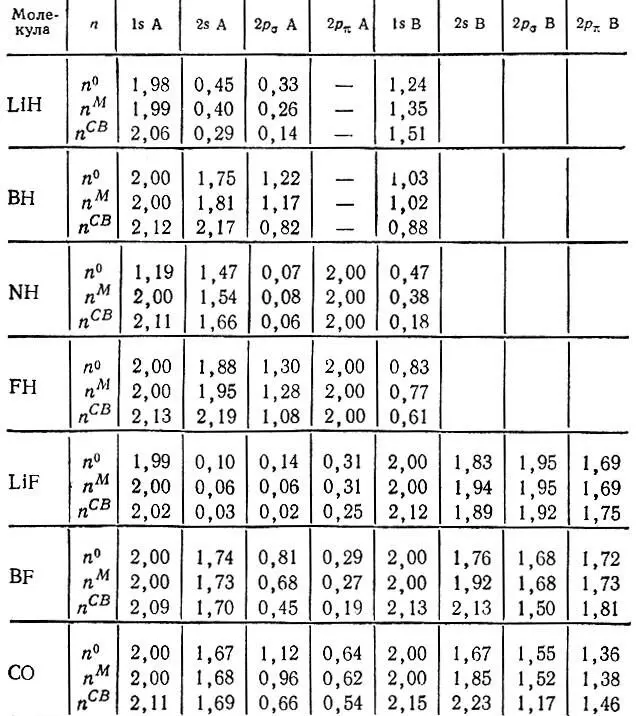
Таблица 11. Заселенности АО n 0, n Mи n CBв двухатомных молекулах LiH, BH, NH, FH, LiF, BF, CO [46]

В химии принято различать одинарные, двойные, тройные, а также связи дробной кратности между атомами, образующими молекулу. Если МО могут быть локализованы на отдельных атомах и двухцентровых связях, то под кратностью связи двух атомов (А и В) естественно понимать число МО, локализованных на связи АВ. В случае молекул, обладающих неспаренными электронами, т. е. находящихся в основных или возбужденных состояниях с отличной от нуля мультиплетностью по спину, следует говорить о локализации спин-орбиталей и отождествлять с кратностью связи половину числа локализованных на ней молекулярных спин-орбиталей (МСО). В качестве примера можно привести ряд двухатомных гомонуклеарных молекул, для котоых локализованные МО (или МСО) являются либо орбиталями неподеленных электронных пар, либо связывающими двух-центровыми орбиталями (табл. 12).

Таблица 12. Кратности связей в некоторых гомонуклеарных молекулах

Однако такой подход к проблеме молекулярно-орбитальной интерпретации понятия кратности химической связи весьма ограничен двумя существенными причинами. Во-первых, локализация МО в орбитали неподеленных электронных пар и двухцентровые связывающие МО, как правило, не является строгой. Во-вторых, локализованные двухцентровые МО могут быть поляризованы, т. е. принадлежать одному из связанных атомов в большей степени, чем другому. При этом исчезает грань между полярной двухцентровой МО и орбиталью неподеленной электронной пары.