Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

Эти причины обусловливают нецелочисленность кратности химических связей в многоатомных молекулах независимо от (того, какой спиновой мультиплетностью характеризуются их состояния. Как частичная делокализация МО, относящихся к некоторой связи, так и их поляризация в направлении любого из связанных атомов должны означать уменьшение кратности этой связи. В то же время делокализация МО, относящихся к другим связям, может вносить определенный вклад в кратность рассматриваемой связи.

Для учета указанных эффектов необходимо квантовохимическое определение кратности химической связи. К настоящему времени в квантовой химии используют довольно много различных индексов, характеризующих химическую связь двух атомов в молекуле, но не все из них соответствуют классическому понятию кратности химической связи. Хотя кратность химической связи не должна быть целочисленной, она должна быть все же величиной неотрицательной (нулевая кратность связи АВ означает отсутствие химической связи между атомами А и В) и инвариантной относительно унитарных преобразований (в частности, поворотов и гибридизации) атомных орбиталей отдельных атомов. Для гомонуклеарных двухатомных молекул квантово-химическое определение кратности должно обеспечивать целые или полуцелые ее значения (см. табл. 12).

Сформулированным условиям удовлетворяет определение кратности химической связи (КА В) согласно равенству [3]:

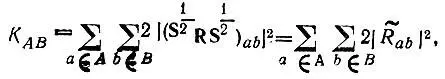(4.90)

где S— матрица перекрывания всех АСО атомов, образующих молекулу; R— матрица, представляющая в базисе этих АСО электронную плотность, точнее ее компоненту, соответствующую максимальному значению проекции полного спинового момента электронов молекулы на ось квантования; а и b — индексы спин-орбиталей атомов А и В.

При отсутствии одноэлектронного спин-орбитального взаимодействия матрица 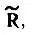, определяемая формулой

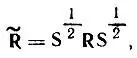(4.91)

имеет квазидиагональный вид

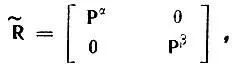(4.92)

где Р αи Р β— одноэлектронные матрицы плотности, соответствующие проекциям спинового момента + 1/ 2и - 1/ 2. С учетом последнего равенства К АВможно представить в виде

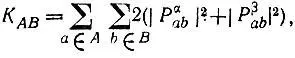(4.93)

а также выразить через матричные элементы электронной (Р) и спиновой (Q) плотности [4]. При этом

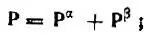(4.94)

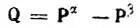(4.95)

и

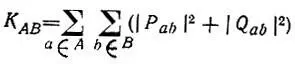(4.96)

Первый член в правой части этой суммы называется индексом Виберга [88] и используется для характеристики химических связей в молекулах с замкнутыми электронными оболочками, если расчет их структуры проводится в рамках приближения нулевого дифференциального перекрывания (S = I) (табл. 13).

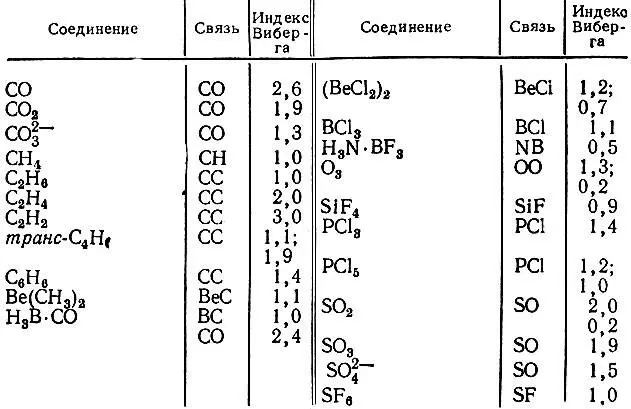
Таблица 13. Индексы Виберга для некоторых соединений элементов первых трех периодов периодической системы [30]

Альтернативное квантовохимическое определение кратности химической связи было предложено в работе [42]. Согласно этому определению

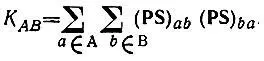(4.97)

В классической теории химической связи каждому атому молекулы сопоставляется определенная валентность, понимаемая как число, характеризующее состояние атома в этой молекуле. Распределение валентности V Aатома A по связям его с остальными атомами молекулы описывается кратностями связей K AB, причем

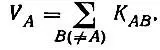(4.98)

Подставляя в это равенство выражение (4.90)$ можно определить V Aчерез матричные элементы Rи S[3]:

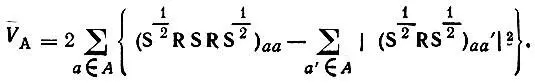(4.99)

В однодетерминантном приближении для молекул, обладающих лишь замкнутыми электронными оболочками, выражение для валентности приводится к виду

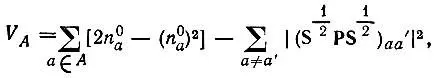(4.100)

где 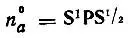— электронная лёвдинская заселенность а-й орбитали, принадлежащей атому А. Последняя сумма может быть исключена из выражения для V Aунитарным преобразованием (гибридизацией) атомных орбиталей [21].

Другое определение валентности

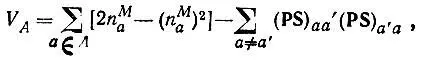(4.101)

где n M a— заселенность АО по Малликену — можно получить, подставляя в равенство (4.98) формулу (4.97).

Уже отмечалось, что n M aможет принимать значения > 2, которые противоречат принципу Паули. Такие неразумные заселенности вносят отрицательный вклад в величину V A. Очевидно, определение валентности атома через лёвдинские заселенности гибридных АО является более предпочтительным. В то же время не следует отказываться и от определения (4.101). Оно может быть полезным в тех случаях, когда в качестве результата расчета электронной структуры химического соединения приводятся заселенности АО по Малликену, а не по Лёвдину, причем опубликованной информации недостаточно, чтобы вычислить последние. Если перекрывание атомных орбиталей мало, то оба определения должны давать близкие результаты.

Систематическое исследование валентностей атомов от водорода до хлора было проведено Армстронгом, Стюартом и Перкинсом [29, 30]. Они показали, в частности, что валентности лития, бериллия и бора превышают номер группы периодической системы, в которой расположены эти Элементы (табл. 14). Интересные результаты были получены для фторидов фосфора, серы и хлора. Валентность указанных элементов оказывается близкой к числу присоединенных ими атомов фтора. В то же время индексы Виберга свидетельствуют о делокализованном характере связей в этих электронно-избыточных соединениях.