Николай Глинка - Общая химия

ΔU = Q v= nC vΔT

Здесь C v— молярная теплоемкость вещества при постоянном объеме; n — количество вещества; ΔT -разность между конечной и начальной температурами.

В случае химической реакции, протекающей без изменения объема системы, изменение внутренней энергии равно взятому с обратным знаком тепловому эффекту этой реакции.

Энтальпия. Однако чаще в химии приходится иметь дело с процессами, протекающими при постоянном давлении. При этом удобно пользоваться величиной энтальпии Н, определяемой соотношением:

H = U + PV

При постоянном давлении и при условии, что в ходе процесса совершается только работа расширения ( A = PΔV )*

ΔH = ΔU + PΔV

или

ΔU = ΔH + PΔV

* Работа (А) против силы внешнего давления равна величине этой силы (F), умноженной на путь (Δl), т.е. A = FΔl. Но сила равна давлению (Р), умноженному на ту площадь (S), на которую оно действует: F = PS, откуда A = PSΔl или A = ΔV.

- 189 -

Сравнивая последнее уравнение с уравнением внутренней энергии

ΔU = Q - A

видим, что при указанных условиях

ΔH = Q p

где Q p— теплота, поглощенная системой при постоянном давлении.

Последнее уравнение дает возможность определять изменение эптальпии при различных процессах. Такие определения аналогичны определениям внутренней энергии, с той разницей, что все измерения должны проводиться в условиях постоянного давления. Так, при нагревании вещества изменение его энтальпии определяется по теплоемкости этого вещества при постоянном давлении

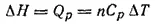
где n — количество вещества; Ср — молярная теплоемкость вещества при постоянном давлении.

При изменениях агрегатного состояния вещества и при аллотропных переходах изменение энтальпии равно по величине, но обратно по знаку теплоте соответствующего превращения (плавление, кипение, превращение из одной модификации в другую). Наконец, в случае химической реакции изменение энтальпии равно взятому с обратным знаком тепловому эффекту реакции, проведенной при постоянной температуре и постоянном давлении.

Энтальпия, как и внутренняя энергия, характеризует энергетическое состояние вещества, но включает энергию, затрачиваемую на преодоление внешнего давления, т. е. на работу расширения. Подобно внутренней энергии, энтальпия определяется состоянием системы и не зависит от того, каким путем это состояние достигнуто. В случае газов различие между ΔU и ΔH в ходе того или иного процесса может быть значительным. В случае систем, не содержащих газов, изменения внутренней энергии и энтальпии, сопровождающие процесс, близки друг к другу. Это объясняется тем, что изменения объема (ΔV) при процессах, претерпеваемых веществами в конденсированных (т. е. в твердом или в жидком) состояниях, обычно очень невелики, и величина PΔV мала в сравнении с ΔH .

Как уже говорилось в § 65, макросостояние системы тем более вероятно, чем большим числом микросостояний оно может осуществиться. Обычно число микросостояний, отвечающих тому или иному макросостоянию системы, очень велико. Это связано с тем, что в макроскопических количествах вещества число частиц колоссально велико, а их положения и скорости при обычных температурах чрезвычайно разнообразны.

Характеризовать в этом смысле состояние системы оказалось удобнее не самой вероятностью осуществления данного макросостояния, а величиной, пропорциональной ее логарифму. Эта величина называется энтропией.

Энтропия (S) связана с числом (W) равновероятных микроскопических состояний, которыми можно реализовать данное макроскопическое состояние системы, уравнением

S = k lg W

где k — коэффициент пропорциональности.

Наименьшую энтропию имеют идеально правильно построенные кристаллы при абсолютном нуле. Энтропия кристалла, в структуре которого имеются какие-либо неправильности, уже при абсолютном нуле несколько больше, так как нарушения идеальности могут реализоваться не единственным способом. С повышением температуры энтропия всегда возрастает, так как возрастает интенсивность движения частиц, а следовательно, растет число способов их расположения. Возрастает она также при превращении вещества из кристаллического состояния в жидкое и, в особенности, при переходе из жидкого состояния в газообразное. Изменяется энтропия и при протекании химических процессов. Эти изменения обычно особенно велики в случае реакций, приводящих к изменению числа молекул газов: увеличение числа газовых молекул приводит к возрастанию энтропии, уменьшение — к ее понижению.

Подобно внутренней энергии и энтальпии, энтропия зависит только от состояния системы. Но, в отличие от этих двух функций, связь изменения энтропии с теплотой зависит от способа проведения процесса — от его скорости.

Как уже говорилось, в ходе того или иного процесса соотношение между теплотой и производимой работой может быть различным. Только разность этих величин, равная изменению внутренней энергии системы, не зависит от способа осуществления процесса. При быстром его проведении работа бывает малой, а при медленном она возрастает. При бесконечно медленном осуществлении процесса — при проведении его бесконечно малыми шагами от одного состояния равновесия к следующему, бесконечно близкому к предыдущему, — работа принимает максимально возможное значение. Такое проведение процесса называется термодинамически обратимым, или просто обратимым.

В ряде случаев к обратимому проведению процесса можно приблизиться в экспериментальных условиях с высокой точностью. В лаборатории можно практически обратимо проводить окислительно-восстановительные реакции в гальванических элементах, (см. § 98), плавление твердого тела, испарение жидкости.

Если процесс проводится обратимо и при постоянной температуре (изотермически), то изменение энтропии связано с поглощаемой теплотой уравнением

ΔS = Q обр/T

где Q обр— количество теплоты, поглощенной системой в изотермическом обратимом процессе; Т — абсолютная температура.

С помощью этого уравнения можно определить, например, изменение энтропии при плавлении и кипении веществ.

Последите уравнение показывает, что при поглощении некоторого количества теплоты энтропия системы возрастает тем сильнее, чем ниже температура, при которой поглощается теплота. Это можно пояснить следующим образом. Подведем одно и то же количество теплоты к двум одинаковым порциям данного вещества. При этом пусть одна из порций находится при низкой температуре, например 1 К, а другая — при высокой температуре, например 1000 К. Ясно, что относительное возрастание скорости движения частиц и увеличение степени их неупорядоченности, а следовательно, и возрастание энтропии в первом случае будет больше, чем во втором.