Борис Штерн - Прорыв за край мира

Теперь вспомним лямбда-член, введенный Эйнштейном в попытке стабилизировать нестационарную Вселенную. Он традиционно обозначается греческой «лямбда», откуда и получил свое название (альтернатива — космологическая постоянная), и фигурирует в уравнениях следующим образом:

R μν —Rg μν — 8 πΛg μν = 16 πT μν/c 4

Он тоже имел расталкивающий эффект и был по определению константой во всем пространстве. Уравнение Фридмана с лямбда-членом в отсутствие материи и в пренебрежении кривизной пространства выглядит так:

( ȧ/a ) 2— 8 π /3 · GΛ = 0,

где а — масштабный фактор, ȧ — его производная по времени. Уравнение Фридмана без лямбда-члена, но со скалярным полем, вошедшим в уравнение через тензор энергии-импульса:

( ȧ/a ) 2 = 8 πG /3ε

Да ведь это абсолютно то же самое, если в постоянно во времени и пространстве и если положить Λ = ε ! Так лямбда-член, забракованный Эйнштейном, вернулся в историю благодаря развитию теории поля, на сей раз в правую часть уравнения, через тензор энергии-импульса.

Каким будет решение уравнения Фридмана, приведенного выше? Конечно, экспонента: а = е t , где t , напомним, — безразмерное время, выражаемое через обычное время, как t = t rH ; Н — постоянная Хаббла, которая в данном случае не меняется со временем: H = √(8 ωG /3 ε ).

Это решение носит имя де Ситтера, а умозрительная соответствующая ему вселенная называется «миром де Ситтера». Это несколько странный мир. Несмотря на экспоненциальный рост масштаба, в нем ничего не меняется. В нем нет глобальной выделенной системы отсчета (а в нашей Вселенной она есть — та, что связана с усредненным движением галактик и реликтовым излучением). Там непонятно, как определить причинно связанную область — горизонт. Более того, для мира де Ситтера можно преобразовать координаты так, что он будет вообще стационарным.

Странности этого мира снимаются малейшим отклонением от вакуумного состояния.

Если там есть хоть немного обычной материи, если скалярное поле и его плотность хоть чуть-чуть меняются во времени или пространстве, сразу экспоненциальное расширение становится реальным, хотя закон расширения будет чуть-чуть отличаться от экспоненты (см. врезку и рис. 13.1). Сразу исчезает стационарность, появляется выделенная глобальная система отсчета и многое другое.

Переход от чисто вакуумного состояния р = -ε к близкому, например р = -0,99 ε , описан на врезке и проиллюстрирован на рис. 13.1. Переход достаточно плавен, но есть и серьезное отличие — где-то прошлом степенная зависимость упирается в ноль, а в будущем сильно отклоняется вниз. Кстати, теоретики рассматривают возможность р < -ε . При этом нарушается так называемый принцип изотропной энергодоминантности, который кажется естественным, но напрямую ниоткуда не следует. Субстанция с таким уравнением состояния называется «фантомной материей», или «фантомной энергией» (второй вариант названия употребляется чаще). Подобный экзотический случай также проиллюстрирован на рис. 13.1: кривая в будущем отклоняется вверх от экспоненты и за конечное время уходит в бесконечность. Это так называемый «Большой разрыв» — страшилка, которую очень любят журналисты (Вселенную вплоть до атомов и нуклонов разорвет на элементарные частицы).

Фактически, сейчас мы наполовину раскрыли карты. Ускоренное расширение Вселенной — тот стержень, вокруг которого будет разворачиваться сюжет в следующей части. Но эта книга не детектив, и стержня мало — нужны еще конкретные сценарии с деталями, в которых может скрываться дьявол.

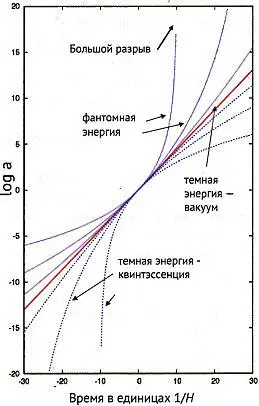
Рис. 13.1. Ход расширения пространства в зависимости от уравнения состояния содержимого вселенной. По горизонтали — время, выраженное в единицах 1/ H 0, где H 0— постоянная Хаббла в момент t = 0. По вертикали — десятичный логарифм масштабного фактора. Центральная красная линия — вакуумное уравнение состояния p = -ε , ему соответствует точная экспонента. Снизу от нее идут кривые для р = -0,9 ε , -0,97 ε , -0,99 ε (в порядке приближения к экспоненте). Сверху, соответственно, идут кривые для р = -1,1 ε , -1,03 ε ,-1,01 ε , что соответствует фантомной энергии

Как решаются самые простые дифуры

Поскольку автор намерен помочь читателям (хотя бы тем, которые помнят что-нибудь о производных) всерьез разобраться, откуда берется ускоренное расширение Вселенной и как работает механизм космологической инфляции, на данной врезке подробно объяснено, откуда берутся приведенные в тексте решения уравнения Фридмана. Первое, что нужно знать, как выглядит производная степной функции у = х β( β — любое фиксированное число). Вот так: dy/dx = βх β-1. Уравнение Фридмана для нулевой кривизны с учетом уравнения состояния и при использовании безразмерного времени (выраженного через постоянную Хаббла) выглядит так:

da/dt = a α,

где а — масштабный фактор, а зависит от уравнения состояния вселенной. Решение ищется в виде

а = c(t+t 0) β,

где с и t 0— константы. Подставляем в уравнение Фридмана:

βc(t+t 0) β-1 = c α (t+t 0) αβ

Понятно, что степени у переменной справа и слева должны быть равны:

β -1 = αβ ,

откуда

β = 1/(1- α )

и

с = (1/ β ) β

На константу t 0пока не обращаем внимания. Обратить внимание надо на случай a = 1, когда b обращается в бесконечность. В этом случае исходное уравнение превращается в

da/dt = а.

Это не только самое простое, но и самое знаменитое дифференциальное уравнение, описывающее размножение нейтронов при ядерном взрыве или бактерий в благоприятной среде. Его решение

a = e t

основано на свойстве экспоненты оставаться самой собой при дифференцировании. Однако, предметом разбирательства остается переход между экспоненциальным и степенным решением. Он из соображений здравого смысла должен быть плавным, а из формул этого не видно. Здесь надо вспомнить про константу t 0. Добавим ее так, чтобы решение при t = 0 совпадало с экспоненциальным. Надо получить а = 1 при t = 0 и для этого взять t 0= β :

a = (1/ β ) β( t + β ) β= (1+ t/β ) β

А теперь надо вспомнить определение числа е и убедиться, глянув в учебник или «Википедию», что последнее выражение при b стремящемся к бесконечности (что происходит, когда а стремится к 1 из-за того, что уравнение состояния вселенной стремится к вакуумному), стремится к e t . Решения для значений а близких к 1 (или больших значений Ь ) показаны в логарифмическом масштабе на рис. 13.1.