Вадим Романов - Прикладные аспекты аварийных выбросов в атмосферу

Получаем:

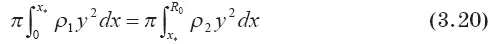
В этом выражении:

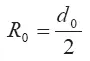— радиус сопла;

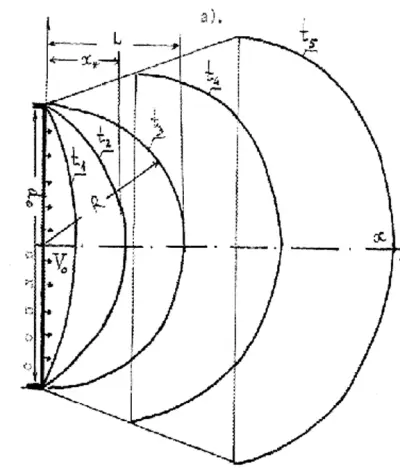
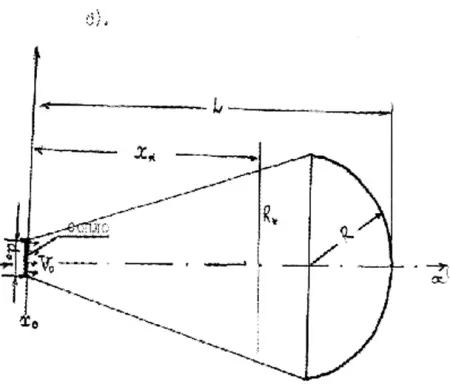
Рис. 3.4. Схема формирования кратковременного выброса при истечении газа из сопла: а) переходный процесс возникновения выброса в окрестности сопла; б) развитый самоподобный выброс.

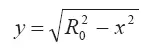— уравнение образующей полусферической поверхности выброса;

ρ 1и ρ 2— плотности газа в левой (х ≤ х *) и правой (х > х *) части выброса, соответственно.

Если предположить, что вещество выброса имеет одинаковую плотность в разных его частях, т. е. ρ 1= ρ 2, то приходим к уравнению относительно искомой координаты центра массы х *. Получаем:

В уравнении (3.21): 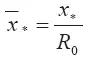— безразмерная продольная координата центра масс.

Решением уравнения (3.21) является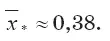

Необходимо отметить, что координата 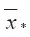, полученная выше, не зависит от метеоданных и степени турбулентности атмосферы. Это объясняется принятой нами моделью «раздувания» выброса в первые мгновения истечения до полусферического объема без вовлечения окружающего воздуха.

При рассмотрении дальнейшей эволюции выброса координата его центра масс будет функцией угла расширения его конической части, т. е. будет зависеть от турбулентности атмосферы. Для ее нахождения обратимся к Рис. 3.46.

Как следует из него в предложении однородности вещества выброса объем усеченной части выброса до координаты х„должен быть равен сумме объемов остальной части выброса.

Важной характеристикой при расчетах продольной координаты центра масс кратковременного выброса х *является х с— координата его центра масс, совпадающая с точкой сопряжения его конической и сферической частей. Важность знания х собъясняется существенной разницей в форме выброса в зависимости от того, больше или меньше значение текущей продольной координаты значения х с. Найдем выражение для х с.

Координаты сопряжения х сконической части выброса со сферической определяется приравнивания объемов этих частей выброса.

Получаем: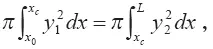

где

у 1= кх — уравнение образующей конической поверхности выброса;

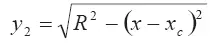— управление поверхности сферической его части.

Подставив значения у 1и у 2в это соотношение, получаем:

Вещественный корень этого уравнения может быть определен по формуле Кардана [172]:

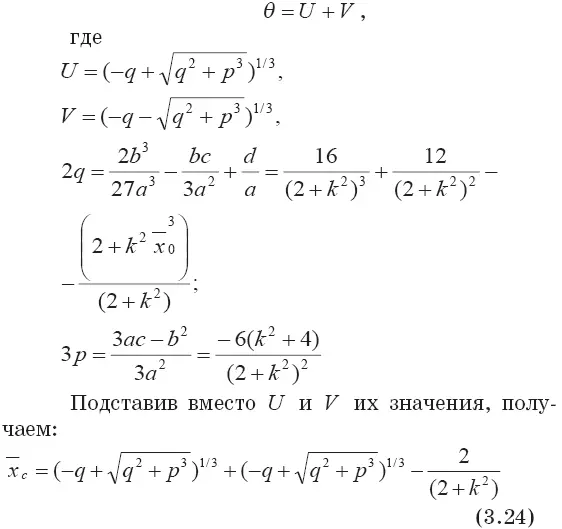
Окончательное выражение для безразмерной продольной координаты сопряжения конической и сферической частей выброса может быть получено при подстановке в соотношение (3.24) вместо р и q их значений. Из-за громоздкости мы его не приводим.

Если известен радиус полусферической «шапки» выброса R, то выражение для продольной координаты сопряжения может быть записано в виде компактного соотношения. Приравниваем объем цилиндрической части выброса

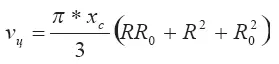
и его сферической части

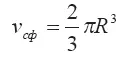
Получаем:

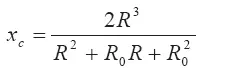
Из рассмотрения Рис. 3.4 видно, что по мере развития выброса координата его центра масс перемещается с полусферической его части на цилиндрическую часть. В математическом виде это утверждение может быть записано так:

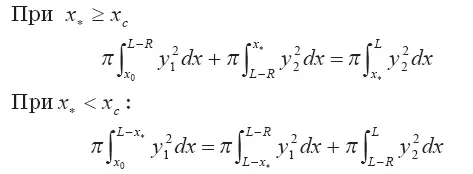
В этих соотношения, как и ранее:

у х=кх — уравнение цилиндрической образующей конуса;

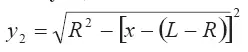— уравнение образующей сферической части поверхности выброса.

После вычисления интегралов имеем следующие соотношения для определения координаты х *:

При х *≥ х с:

v 1+ v 2= v 3(3.25)

где

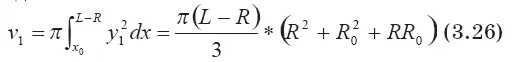
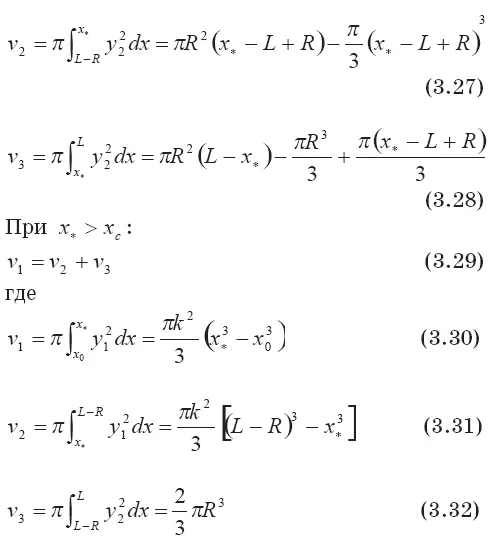
Уравнение (3.25) при учете вида соотношений (3.26), (3.27), (3.28) записывается в виде кубического уравнения

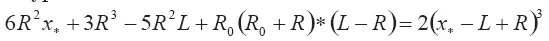
В каноническом виде относительно переменной

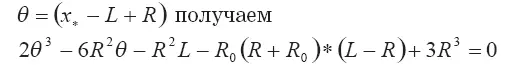
Это уравнение при учете связи характеристик выброса R и L может быть решено аналитически или численно.

Уравнение (3.29) при учете соотношений (3.30), (3.31), (3.32) записывается так:

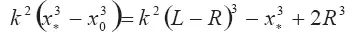
Откуда

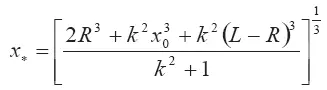
или при учете соотношения

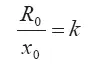
получаем для х *окончательное выражение (случай х *<���х с):

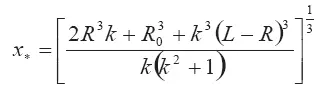
Поперечный размер выброса в месте нахождения его центра масс R„может быть определен при использовании геометрических построений Рис. 3.4.