Вадим Романов - Прикладные аспекты аварийных выбросов в атмосферу

Здесь, как и ранее, радиус полусферической «шапки» выброса определяется соотношением:

При большом времени истечения вещества из сопла кратковременный выброс перестраивается в струйный. Для струйного выброса значением начального радиуса R 0можно пренебречь по сравнением с его приращением, т. е.

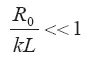
При этом

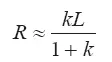
и из соотношения (3.29) при учете (3.30), (3.31) и (3.32) получаем асимптотические зависимости для координат центра масс выброса

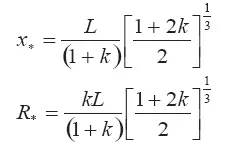
График зависимости безразмерной координаты центра масс струйного выброса 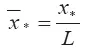от коэффициента углового расширения его конической части к представлен на рисунке 3.5.

Как следует из графика этого рисунка увеличение угловой координаты его центра масс приводит к линейному уменьшению 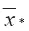. Однако, эта зависимость сравнительно слабая. В диапазоне возможных состояний атмосферы, характеризующихся диапазоном коэффициентов углового расширения 0,087 ≤ к ≤ 0,364 (классы устойчивости атмосферы от В до Е по классификации Пасквилла) безразмерное значение продольной координаты изменяется от

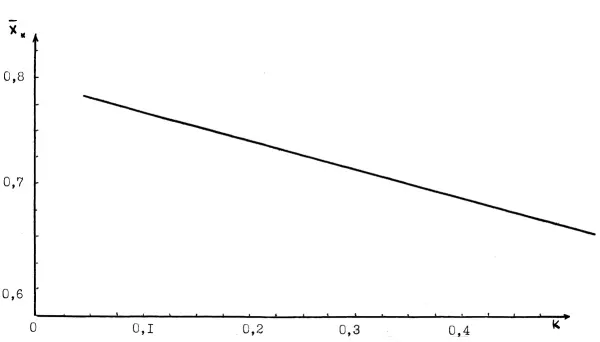
Рис. 3.5. Зависимость безразмерной продольной координаты струйного выброса продуктов горения из сопла от углового коэффициента расширения струи к.

Найдем теперь выражение для поверхностей вовлечения формирующихся кратковременных выбросов. Считаем, что выходящий из сопла газ механически выдавливает окружающий воздух вплоть до полусферического объема (это состояние вещества выброса соответствует временной координате t 3на Рис. 3.4а). Вовлечение в выброс начинает происходить при t > t 3через образующуюся коническую его поверхность.

Площадь вовлечения окружающей среды при этом запишется так:

S B= π (R + R 0) × L .обр

где

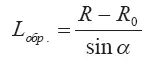длина образующей конической поверхности,

α — угол конической поверхности выброса.

Учитывая связь угла а и коэффициента углового расширения потока к:

к = tgα

находим для образующей следующее L обрвыражение:

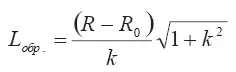
Подставляя в выражение для площади вовлечения вместо L обрего выражение, получаем:

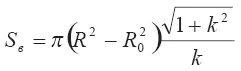
При учете формулы для радиуса R получаем окончательное выражение для поверхности вовлечения кратковременного выброса. Оно имеет вид:

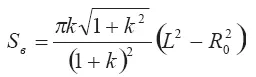
На графике Рис. 3.6 представлена зависимость безразмерной (отнесенной к площади соплового сечения) поверхность вовлечения кратковременного выброса от безразмерной длины выброса для различных значений углового расширения к:

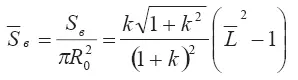
Как следует из этого графика, безразмерная поверхность вовлечения 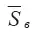растет с увеличением безразмерной длины выброса 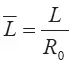. Увеличение угла расширения потока (фактически коэффициента вовлечения) приводит к более резкому возрастанию .

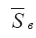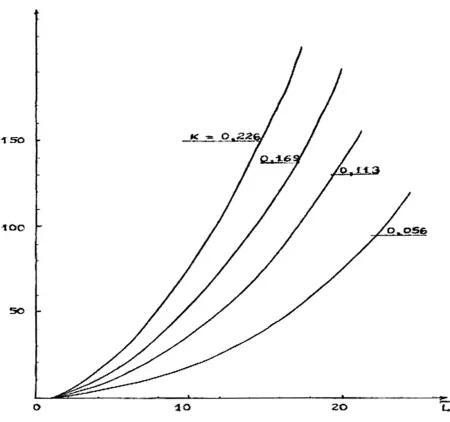
Рис. 3.6. Зависимость безразмерной площади вовлечения в кратковременный выброс от его безразмерной длины для различных значений коэффициента углового расширения потока.

Вычислим теперь объем кратковременного сформировавшегося выброса, состоящего из усеченного конуса и полусферы. Получаем:

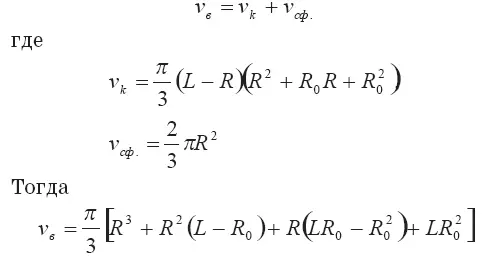
или подставляя вместо R его значение из (3.33), можно получить выражение для объема выброса через его длину и начальный радиус R 0. После громоздких вычислений находим:

При решении задач подъема в атмосфере неизотермических струй и клубов загрязняющих примесей, возникающих при штатной работе и авариях на промышленных объектах, необходимо знать некоторые интегральные характеристики выброса и ветрового потока.

В частности, в уравнения движения струи или клуба в сносящем потоке входят коэффициент вовлечения окружающей среды в выброс g и параметр, характеризующий отклонение струйного потока как целого от ветра — С х.

Рассмотрим сопротивление струи в ветровом потоке, определяемое коэффициентом аэродинамического сопротивления С х.

В литературных источниках существуют подходы, когда газообразное «тело» струи заменяют эквивалентным твердым цилиндром, обладающим соответствующим коэффициентом С х, либо считают, что на самом деле из-за вовлечения в струю сносящего потока ее коэффициент С хбудет отличаться от С хсоответствующего твердого тела, т. к. ветровой поток передает струе свой импульс.

Для выяснения физического смысла этого параметра и его числовых значений рассмотрим условие динамического равновесия контрольного газообразного элемента струи Δν в ветровом потоке в проекции на ось х.

Объем Δν ограничен сечениями «1» и «2» (Рис. 3.7), имеет длину Δl и радиус R. Приравниваем изменение количества движения рассматриваемого элемента Δν импульсу действующей на него силы аэродинамического сопротивления F A. Получаем за интервал времени: