Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Дифракция рентгеновских лучей на кристаллах

Какой же физический принцип лежит в основе изучения структуры кристаллов посредством метода дифракции рентгеновских лучей? Когда на кристалл падает излучение, длина волны λ которого равна расстоянию между атомами (доли нанометра), то имеет место явление, аналогичное тому, которое возникает при прохождении пучка световых лучей через отверстия Юнга (см. главу 3, «Интерференция и когерентность»): атомы кристалла рассеивают рентгеновские лучи, также как щели Юнга рассеивают свет. Кристалл ведет себя как регулярная решетка, образованная из большого количества щелей Юнга (см. илл.). Лучи, рассеянные атомами, интерферируют.

В любой нерегулярной среде такая интерференция обычно деструктивна: рассеиваемые волны практически полностью гасят друг друга, за исключением направления распространения падающего луча. В кристалле же, из-за периодичности структуры, помимо направления распространения падающего луча, существуют различные другие выделенные направления, для которых волны, переизлучаемые атомами, находятся в фазе. Наличие таких направлений указывает на существование плоскостей, проходящих через большое количество точек кристаллической решетки, так называемых кристаллографических плоскостей.

Конструктивная интерференция возникает тогда, когда рассеянные лучи удовлетворяют равенству, называемому условием Вульфа – Брэгга:

2 d sin θ = n λ,

где d – расстояние между двумя кристаллографическими плоскостями, θ – угол между падающим лучом и кристаллографической плоскостью и n – любое целое число.

На опыте при использовании условия Вульфа – Брэгга положение кристалла остается неизменным по отношению к направлению пучка падающих рентгеновских лучей, а изменяется длина волны последних. Помещая на пути рассеянных рентгеновских лучей фотографическую пластину, ученые получают дифрактограмму, подобную приведенной здесь: светлые пятна соответствуют направлениям, для которых выполняется условие Вульфа – Брэгга. Этот метод был разработан Максом фон Лауэ (1879–1960) и принес ему Нобелевскую премию по физике 1914 года.

Независимо от направления кристаллографических плоскостей всегда существует такое значение длины волны излучения, которое позволяет удовлетворить условию Вульфа – Брэгга. Изучая дифрактограмму, мы можем найти расстояние d между кристаллографическими плоскостями и определить структуру кристалла, если она достаточно проста. В более сложных случаях необходимо не только определить сами направления конструктивной интерференции, где интенсивность излучения отлична от нуля, но и измерить величину последней.

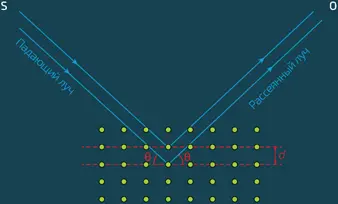
Принцип дифракции рентгеновских лучей на кристаллах.Источник S испускает рентгеновские лучи в направлении кристалла под углом θ к кристаллографическим плоскостям. Наблюдатель в точке O регистрирует интенсивность полученного луча. Две кристаллографические плоскости отстоят на расстояние d , которое соответствует условию Вульфа – Брэгга

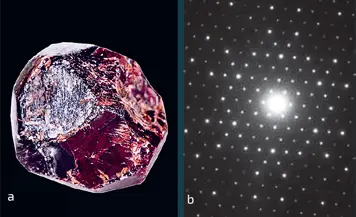
a. Гранат. b.Дифрактограмма граната. Расположение четких пятен дает нам информацию о расположении атомов внутри кристалла

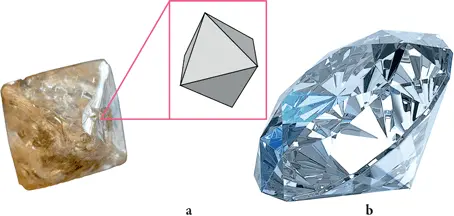
6. Этапы гранения необработанного октаэдрического алмаза (а). Чтобы получить бриллиант (b), огранщик начинает с небольшого надреза в камне, а затем ударяет по введенному в него лезвию, после чего алмаз раскалывается пополам по плоскости расщепления. Затем ювелир путем полировки создает грани (для получения бриллианта в современной огранке их должно быть 58)

С другой стороны, по определению кристалл остается неизменным при бесконечном количестве сдвигов: достаточно выбрать их расстояния и направления, которые соответствовали бы периодичности кристалла. Именно это свойство, трансляционная симметрия, сегодня считается наиболее характерным свойством кристаллов, а не их макроскопическая симметрия, наблюдаемая невооруженным глазом. Красота кристаллов, их сверкающие грани и причудливые формы не могут не восхищать нас, будь то маленький бриллиант в кольце или один из великолепных минералогических шедевров, которыми можно полюбоваться в музеях естественной истории.

Но, кстати, какова связь между микроскопической структурой кристалла и его макроскопической геометрией? Наличие плоских блестящих граней, будь они природными или полученными в результате обработки, – результат регулярности микроскопической структуры. На самом деле совсем не сложно расколоть кристалл, образовав гладкие плоскости: если одна атомная связь слаба, то все связи, имеющие аналогичное положение в кристаллической решетке, будут столь же слабыми. Эту особенность кристаллов используют ювелиры при огранке необработанных алмазов (илл. 6). Формирование плоских граней при росте кристалла может быть объяснено аналогичным образом.

Кристаллы могут иметь оси симметрии порядков 2, 3, 4 или 6… но только не пятого порядка! Исключение числа 5 из этого списка – математически неоспоримое свойство: невозможно заполнить пространство повторяющейся ячейкой с симметрией пятого порядка. Как было отмечено, на плоскости можно замостить тротуар прямоугольниками, шестиугольниками, квадратами или равносторонними треугольниками (см. главу 8, «Упаковка дисков и «замощение» плоскости многоугольниками»), но не пятиугольниками!

Эта аномалия интересует некоторых исследователей, тем более что сама природа, судя по всему, охотно принимает симметрию пятого порядка. Так, она часто встречается в цветах (илл. 7). Она возникает и в небольших скоплениях атомов, получаемых в лаборатории. Исследователям удается получить скопления молекул Al 13 или Al 12 C, образованных из одного центрального и 12 периферийных атомов: они формируют правильный икосаэдр, который имеет оси симметрии пятого порядка (см. илл. b в главе 8, врезке «Поцелуи» шаров в задаче Кеплера»), а не кубоктаэдр, являющийся элементарной ячейкой компактной укладки (илл. а в главе 8, врезке «Поцелуи» шаров в задаче Кеплера»).

Однако даже для бесконечной системы симметрия пятого порядка не является несовместимой с высокой компактностью. Если отказаться от построения периодической структуры с симметрией пятого порядка, то можно довольствоваться расположением, показанным на илл. 8, где шарики каждого слоя расположены на гранях правильных пятиугольников. Полученное заполнение составляет 72 %, что ненамного меньше возможной максимальной величины 74 % (см. главу 8, «Шары в реальном мире»).