Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Эта формула верна только в том случае, когда можно не учитывать воздействие на жидкость силы тяжести, то есть при условии, что все рассматриваемые точки находятся на одной и той же высоте. Далее мы разберемся, как учесть и силу тяжести.

Изменение давления в потоке жидкости, текущей по трубе переменного сечения, легко проверить экспериментально.

Жидкость протекает по трубе с широкой и узкой секциями, каждая из которых снабжена вертикальной трубкой, открытой сверху (см. илл.). Эти трубки играют роль «датчиков давления»: предполагается, что они тонкие и их наличие на свойства потока не влияет.

Когда поток устанавливается, то можно заметить, что высота воды в трубах различна. При этом уровень тем выше, чем сильнее давление в той секции трубы, куда вставлена трубка. Измеряя разницу высот Δ h между сечениями A и C (или между сечениями B и C), можно найти перепад давления Δ P между широкой и узкой секциями на оси основной трубы: Δ P = ρ g Δ h . Зная мощность потока и диаметры секций трубы, легко вычислить скорости, и таким образом можно проверить справедливость теоремы Бернулли.

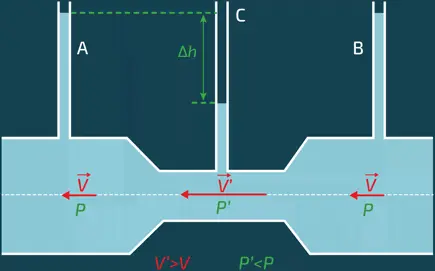
При наличии потока справа налево в горизонтальной трубе уровень жидкости в трубке С ниже, чем в трубках А и В. Этот опыт позволяет нам судить о перепаде давления в жидкости между узкой и широкой частями трубы, связанном с тем, что скорость в узкой части выше (V’ > V). Равенство уровней в сечениях A и B позволяет убедиться в отсутствии «потери мощности на нагрузке», то есть в том, что рассеивание механической энергии жидкости посредством трения незначительно

– Если я правильно понял, – сказал Пол, – теорема Бернулли применима к несжимаемой жидкости, такой как вода. Но ведь воздух в туннеле таким не является!

– Это верно, – ответил Дэниел, – величина P + ρ V 2/ 2 в туннеле не совсем постоянна. Но в целом рассуждение остается правильным: поскольку поток массы остается одинаковым в любой точке трубы, то в узкой ее части воздух вынужден двигаться быстрее. Чтобы его ускорить, требуется сила, и эта сила обусловлена разницей давлений. Поэтому в узкой части возникает область пониженного давления. Это явление называют «эффектом Вентури» в честь итальянского физика, который вскоре после Бернулли изучал действие различных устройств, основанных на движении потока по трубе переменного диаметра.

Пола интересовала еще одна деталь.

Как определить скорость самолета относительно окружающего воздуха? Теорема Бернулли (с некоторыми необходимыми допущениями, поскольку на самом деле воздух не является несжимаемым) сводит это измерение к оценке разности давлений. Последняя осуществляется с помощью трубки Пито, установленной снаружи фюзеляжа. Принцип такого измерения предложил французский физик Анри Пито (1695–1771).

Трубка Пито состоит из двух Г-образных труб, в которых просверлены параллельное (C) и перпендикулярные потоку (B и B’) отверстия.

Величина, которую нужно измерить, – это скорость самолета по отношению к воздуху, которую мы обозначим – V (удобно определять скорость относительно самолета, так что скорость воздуха непосредственно перед самолетом, в точке А, равна V ). При попадании в трубку встречный поток разделяется. Небольшая ее часть, C, заполняется воздухом, скорость которого здесь равна нулю, поскольку трубка заполнена и закрыта на другом конце. Скорость воздуха равна нулю также и в D: таким образом, давление в точках C и D совпадает. Другая часть воздуха обтекает трубу и достигает отверстий B и B’, практически не изменяя свою скорость V , что позволяет определить давление, которое устанавливается в точке F.

Далее с помощью манометра измеряется перепад давления P D – P F между точками D и F, который эквивалентен разнице давлений P C – P B между точками C и B и совпадает с перепадом давления P C – P A . Теперь нам осталось вычислить скорость самолета, используя теорему Бернулли. В случае несжимаемого потока последняя приводит к равенству P C = P A + ρ V 2/2. Поскольку измеренная разность давлений P D – P F равна P C – P A , то скорость самолета оказывается равной:

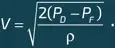
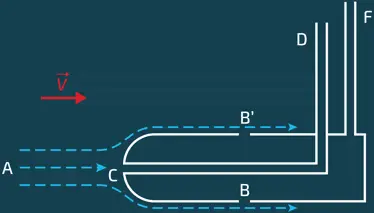
Схема трубки Пито

Трубка Пито, установленная под крылом самолета. Это устройство стало печально известным в июне 2009 года: пилоты рейса Рио-де-Жанейро – Париж, по всей видимости, отреагировали на неверные показания обледеневших трубок Пито, что привело к падению самолета

– Скорость потока в поезде и рядом с ним, очевидно, разная. Почему же давление внутри и снаружи одинаковое?

– Действительно, скорости воздуха внутри и снаружи поезда совсем разные, – признал Дэниел. – Однако если даже одно окно в вагоне затворено неплотно, то давление внутри него станет примерно равным пониженному давлению снаружи. Так, при незакрытом окне его занавески выдувает наружу. На этом явлении основан принцип действия трубки Пито, которую обычно используют для измерения скорости потока (см. главу 10, «Вытекание жидкости из сосуда и советы водопроводчика»). Она фиксирует соответствующие давления с помощью специальных отверстий, а вычислить искомую скорость можно по теореме Бернулли. Эти отверстия можно сравнить с плохо закрытым окном поезда.

– Вот именно! – заметила Клаудия, наша итальянская коллега. – В нашем поезде нет окон: только застекленные световые проемы, которые невозможно открыть!

Подошедший контролер завершил объяснение:

– Высокоскоростные поезда действительно имеют хорошую герметичность. Эффект пониженного или избыточного давления снаружи полностью ощущается нами только спустя некоторое время, порядка десяти секунд…

4. Различные приборы для измерения давления: манометр для проверки автомобильных шин (a), барометр (b) и барометрический высотомер (c). Последний позволяет определить высоту путем измерения атмосферного давления, которое уменьшается с набором высоты (см. главу 15, «Скороварка и готовка на высоте»)