Анатолий Ахутин - История принципов физического эксперимента от античности до XVII века

Филон Византийский, сочинения которого Герон называет наряду с архимедовскими в качестве одного из своих источников, жил в первой половине III в. до н. э. и оставил солидную «Механику» 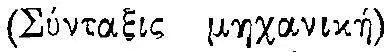. Он, безусловно, находится под влиянием перипатетиков (в начале III в. между перипатетиками и первыми Птолемеями были весьма оживленные контакты, в это же время Филон работал вместе с александрийскими инженерами и математиками на острове Родос 76 ) и ссылается на цитируемое Паппом положение, полученное из механических доказательств и физических оснований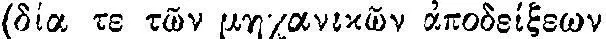 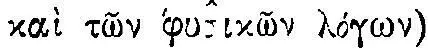во второй книге «Механики» 77 .

Именно эти исследования традиционных кругов привели Архимеда к первоначальной теории рычага и уже от нее — к понятию центра тяжести, который поэтому на первых порах еще смешивается с точкой подвеса. В комментариях Евтохия Аскалонского к трактату Архимеда «О равновесии плоских фигур» говорится: «Момент 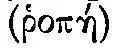...является общеродовым понятием для тяжести и легкости, так говорит Аристотель и, следуя ему, Птолемей... В рассматриваемой книге Архимед называет центром момента 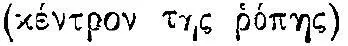плоской фигуры точку, при подвешивании за которую фигура остается параллельной горизонту; центром момента или тяжести двух или более плоских фигур он называет точку подвеса рычага, остающегося параллельным горизонту, если прикрепить к его концам упомянутые фигуры» (с. 68—69). Здесь очень важно слово «момент» 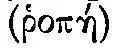, которое позволяет установить непосредственную связь с тем, о чем мы говорили раньше (с. 87). Определение центра тяжести прежде всего как «центра стремлений» впрямую соединяет кинематическую и геометрическую теории. Действительно, безразличное равновесие, это как раз та неразличимость покоя и движения (их безразличие), которое было «первым» для Аристотеля и которое непосредственно отождествляет круг-траекторию и круг-фигуру.

Это объясняет нам также и греческое название трактата: «О равновесии плоских фигур или о центрах тяжести плоских фигур» 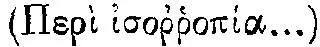или, как переводят немцы,— о равнооклонности ( uber Ausgleichung des Neigens ) 7 S . В этом названии последний след динамического происхождения Архимедовой статики.

В 24-й главе I книги «Механики» Герон (см. 5—8 предложение) и в VIII книге «Собрания» Папп воспроизводят те мысленные эксперименты, которые, по-видимому, привели Архимеда к определению центра тяжести.

«...Центром тяжести некоторого тела,— читаем мы у Паппа,— является некоторая расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно 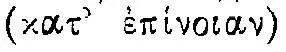подвесить тяжелое тело, то оно остается в покое и сохраняет первоначальное положение» (с. 71). Но как же мы можем произвести это мысленное подвешивание? Как мы можем увидеть эту невидимую внутреннюю точку? Архимед (согласно Герону и Паппу) подробно излагает эту мысленно-экспериментальную процедуру. Основу ее составляет отождествление тела с весами, т. е. мысленное уравновешивание его и нахождение единого центра равновесия всех «весов». «Вообразим,— продолжает Папп,— некоторую вертикальную плоскость... направленную к центру мира, куда, по-видимому, имеют стремление 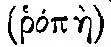все тела, обладающие весом...» и уравновесим тело на ней в разных положениях. Вообразив, далее, различные сечения тела этой плоскостью (в положениях равновесия), мы «увидим», что все они пересекаются в одной точке, которая «и называется центром наклона и тяжести» (с. 71). Поскольку мысленный эксперимент не дает возможности просто увидеть «факт» (пересечения всех плоскостей в одной точке), он необходимо связан с некоторым доказательством, т. е. в данном случае, например, с рассмотрением, что получится, если будут две точки пересечения, и с опровержением этой возможности.

В результате мы получаем предметно-теоретическое понятие центра тяжести, т. е. центра, вокруг которого (на концентрических окружностях) располагаются уравновешенные части.

Следующий шаг приводит нас в центр всей конструктивной, геометро-механической мысли Архимеда. Если теперь мы возьмем геометрическую фигуру — «равномерную по толщине и однородную по весу» (Герон. Механика, II, 35, с. 73),— то разделение ее (по разным направлениям) на две равновеликие части будет соответствовать ее уравновешиванию. Чисто геометрическая операция заменяет здесь механическую.

Вот, что такое геометризация механики, произведенная Архимедом, и вот почему понятие центра тяжести, т. е. точки, действие которой на плечо рычага эквивалентно действию всего протяженного тела, является важнейшим для понимания вывода закона рычага. Поэтому-то 4, 5 и 7 допущения, 4, 5 и 8 предложения трактата «О равновесии плоских фигур» касаются центра тяжести, и 9—15 предложения первой книги и вся вторая книга (за исключением 9-го предложения) посвящены определению геометрических свойств центров тяжестей различных плоских фигур.

Любопытно было бы задать вопрос, является ли понятие центра тяжести математическим или физическим в смысле Аристотеля. Является ли оно понятием точки, поскольку она связана с материей, или же точки как абстрактного математического элемента? Не встречаемся ли мы здесь снова и в гораздо более явной форме с тем, что именно математическая идеализация выражает физическую сущность вещи? И не является ли механическая сущность геометрии тем, благодаря чему математика воспринимает «физическую интуицию»?

Архимед дает нам блестящий пример такого взаимоперехода. Если действие тела на плечо рычага сводится к действию его центра тяжести, то при однородном распределении тяжести по объему, что можно представить только в случае идеальной геометрической фигуры, равновесие есть равновеликость, и мысленное взвешивание геометрических фигур становится универсальным методом решения традиционной задачи греческой геометрии: сравнения фигур по величине.