Карло Ровелли - Нереальная реальность. Путешествие по квантовой петле

Уравнение Дирака.

Существует явление, которое, по-видимому, не сводится к Стандартной модели, – темная материя. Астрофизики и космологи наблюдают во Вселенной влияние особого типа материи, которая, похоже, не описывается Стандартной моделью. Там вообще еще немало вещей, о которых мы не знаем.

Я считаю, что утверждение, будто бозон Хиггса «объясняет массу», несколько преувеличено. Бозон Хиггса ничего не «объясняет» относительно происхождения массы. Что же он все-таки говорит о массе? Это чисто технический момент: Стандартная модель предполагает некоторые симметрии, и эти симметрии, по-видимому, позволяют существовать лишь безмассовым частицам. Хиггс с коллегами поняли, что можно получить одновременно и симметрии, и массы, если вводить последние косвенным образом, через взаимодействие с определенным полем, известным сегодня как поле Хиггса.

Конечная область фазового пространства – пространства возможных состояний системы – содержит бесконечное число различимых классических состояний, но всегда только конечное число ортогональных квантовых состояний. Это число находится путем деления объема области на постоянную Планка в степени, равной числу степеней свободы. Этот результат носит общий характер.

Соответствующий фрагмент в переводе Ф. А. Петровского:

Цит. по: Лукреций . О природе вещей. – М.: Изд-во АН СССР, 1946. – С. 84–85. – Примеч. пер .

Или фейнмановским интегралом. Вероятность перемещения из точки A в точку B равна квадрату модуля интеграла по всем путям от экспоненты классического действия вдоль траектории, умноженного на мнимую единицу и деленного на постоянную Планка.

Обсуждение реляционной интерпретации квантовой механики см. в статье “Relational Quantum Mechanics” («Реляционная квантовая механика»), опубликованной на сайте Stanford Encyclopedia of Philosophy (http://plato.stanford.edu/archives/win2003/entries/rovelli), и в статье Карло Ровелли (Carlo Rovelli), “Relational Quantum Mechanics” в International Journal of Theoretical Physics , 35, 1637, 1996, http://arxiv.org/abs/quantph/9609002.

Специальный механизм на мгновение открывает маленькое окошко в правой части ящика, позволяя фотону вылететь в строго определенный момент времени. Взвесив ящик, можно узнать энергию вылетевшего фотона. Эйнштейн надеялся, что это создаст трудности для квантовой механики, которая утверждает, что время и энергию нельзя точно измерить совместно. Бор ошибочно ответил, что для преодоления этой трудности требуется эйнштейновская общая теория относительности, а Эйнштейн ошибочно согласился с ответом Бора. Правильный ответ Эйнштейну, который Бор не смог найти, но который сегодня ясен, состоит в том, что положение вылетающего фотона и вес ящика остаются связанными друг с другом («коррелированными»), даже когда фотон уже улетел далеко.

Фейнман Р. Характер физических законов. М.: 1987. – С. 117. – Примеч. пер .

Bas van Frassen. Rovelli’s World , in Foundations of Physics , 40, 2010, 390–417; Michel Bitbol. Physical Relations or Functional Relations? A Non-metaphysical Construal of Rovelli’s Relational (Физические отношения или функциональные отношения? Неметафизическая интерпретация реляционной квантовой механики Ровелли) Quantum Mechanics, Philosophy of Science Archives, 2007, http://philsci-archive.pitt.edu/3506/; Mauro Dorato . Rovelli’s Relational Quantum Mechanics, Monism and Quantum Becoming (Реляционная квантовая механика Ровелли, монизм и квантовое становление), Philosophy of Science Archives, 2013, http://philsci-archive.pitt.edu/9964/, and Che cos’è il tempo? Einstein, Gödel e l’esperienza commune ( Что есть время? Эйнштейн, Гёдель и общий опыт ). – Rome, Carocci, 2013.

Работа по измеримости полей Нильса Бора и Леона Розенфельда: Det Kongelike Danske Videnskabernes Selskabs, in Mathematiksfysike Meddelelser , 12, 1933.

Черточка на h в постоянной Планка служит лишь для указания, что в этом уравнении постоянную Планка надо разделить на 2π, – довольно бесполезное специфическое добавление, придуманное физиками-теоретиками, которые считают, что эта маленькая черточка на букве h «делает ее элегантной».

Matvei Bronštejn. Quantentheorie schwacher Gravitationsfelder, in Physikalische Zeitschrift der Sowjetunion , 9, 1936, 140–157; и «Квантование гравитационных волн» // Письма в ЖЭТФ. 1936. T. 6. С. 195–236.

См.: F. Gorelik and V. Frenkel. Matvei Petrovich Bronstein and Soviet Theoretical Physics (Boston, Birkhauser Verlag, 1994). Кстати, настоящая фамилия Троцкого был Бронштейн. (См.: Горелик Г. Е., Френкель В. Я. Матвей Петрович Бронштейн. 1906–1938. М., 1990. – Примеч. пер .)

Франческо Петрарка . На жизнь Мадонны Лауры. XC (пер. Е. Солоновича). – Примеч. пер .

Чтобы услышать эту метафору в изложении самого Уилера, зайдите на сайт http://www.webofstories.com/play/9542?o=MS.

Об этом эпизоде вспоминает Брайс Девитт, http://www.aip.org/history/ ohilist/23199.html.

Девитт заменил производные дифференциальными операторами в уравнении Гамильтона – Якоби для общей теории относительности (выведенном незадолго до того Пересом). Тем самым он сделал то же, что и Шрёдингер для вывода своего уравнения в своей первой работе: заменил производные дифференциальными операторами в уравнение Гамильтона – Якоби для частицы.

Или уравнением Эйнштейна – Шрёдингера.

Самая известная альтернатива петлевой квантовой гравитации – это теория струн, основное назначение которой не столько в изучении квантовых свойств пространства и времени, сколько в поиске объединенной теории всех известных полей, цель, быть может, несколько преждевременная при современном уровне знаний.

Собственное значение уравнения для оператора объема.

Поскольку квантовые состояния гравитации выражаются как, где n относится к узлам, а l – к ребрам графа.

Результат расчета прост. Я продемонстрирую его здесь, чтобы вы увидели, как работает дираковский спектр. Возможные значения площади A даются следующей формулой, где j принимает полуцелые значения, то есть 0, 1/2, 1, 3/2, 2, 5/2, 3…

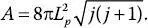
Здесь A – площадь, которую может иметь поверхность, разделяющая два «зерна» пространства; 8 – это обычное число восемь, ничего особенного; π – греческая буква пи, которая, как мы учили в школе, означает отношение длины любой окружности к ее диаметру; эта величина почему-то постоянно появляется в разных разделах физики. L p – это планковская длина, то есть предельно малый размер, на котором проявляются эффекты квантовой гравитации. L 2 p – это квадрат величины L p , который соответствует (чрезвычайно малой) площади крошечного квадрата со сторонами, равными планковской длине. Таким образом, 8π L 2 p – это просто «маленькая» площадь, площадь микроскопического квадрата со стороной примерно в одну миллионную миллиардной миллиардной миллиардной доли сантиметра (10 –66см 2). Интересная особенность этой формулы – квадратный корень в ней. Ключевой момент здесь – то, что j принимает полуцелые значения, то есть кратные 1/2. Например, для каждого из них данный корень приобретает определенные значения, которые в приближенном виде даны в табл. 6.1.