Ричард Фейнман - Том 1. Механика, излучение и теплота

Совершенно ясно, что для движения одной частицы мы получаем и три уравнения для трех плоскостей. Более того, если мы складывали такие величины, как хр у — ур x , для многих частиц и называли это полным угловым моментом, то теперь у нас есть три сорта подобных выражений для трех плоскостей: ху, yz и zx , а сделав то же самое с моментами сил, мы можем также говорить и о полных моментах сил в этих плоскостях. Таким образом, появляются законы о том, что внешний момент сил в некоторой плоскости равен скорости изменения углового момента в той же плоскости. Это просто обобщение того, что писалось для двух измерений.

Однако теперь можно сказать: «Но ведь есть еще и другие плоскости. Разве нельзя в конце концов взять плоскость под каким-то углом и вычислять действующие в ней моменты сил. Для каждого такого случая нужно писать другие системы уравнений, так что в результате их наберется масса!» Здесь следует отметить очень интересное обстоятельство. Оказывается, что если мы в комбинации x ' F y '- y ' F x 'для «косой» плоскости выразим величины x', F y 'и т. д. через их компоненты, то результат можно записать в виде некоторой комбинации трех моментов в плоскостях ху, yz и zx . В этом нет ничего нового. Другими словами, если нам известны три момента сил в плоскостях ху, yz и zx, то момент сил в любой другой плоскости, как и угловой момент, может быть записан в виде их комбинации: скажем, 6% одного, 92% другого и т. д. Этим свойством мы сейчас и займемся.

Пусть Джо для своих координатных осей x, y , z определял все моменты сил и все угловые моменты во всех плоскостях. Однако Мик направил свои оси х ', у ', z ' по-другому. Чтобы немного облегчить задачу, предположим, что повернуты только оси x и y. Мик выбрал другие оси х ' и у ', а его ось z осталась той же самой. Это означает, что плоскости yz и zx у него новые, а поэтому моменты сил и угловые моменты у него тоже окажутся новыми. Например, его момент сил в плоскости х ' у ' окажется равным x ' F y '- y ' F x ' и т. д. Следующая задача — найти связь между новыми и старыми моментами сил. Ее вполне можно решить, установив связь одного набора осей с другим. «Да это же напоминает то, что мы делали с векторами»,— скажете вы. Действительно, я собираюсь делать в точности то же самое. «А не вектор ли он, этот момент сил?» — спросите вы. Действительно , он — вектор, однако этого нельзя сказать просто так, без всякого математического анализа. Так что следующим этапом должен быть анализ. Однако мы не будем подробно обсуждать каждый шаг, а только покажем, как это все работает. Моменты сил, вычисленные Джо, равны

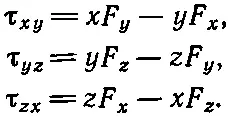(20.1)

В этом месте мы сделаем отступление и заметим, что в подобных случаях, если оси координат выбраны неправильно, для некоторых величин получается неверный знак. Почему бы не написать τ yz = zF y - yF z ? Этот вопрос связан с тем обстоятельством, что система координат может быть либо «левая», либо «правая». Однако выбрав (произвольно) знак, скажем, у τ xy , можно всегда определить правильное выражение для остальных двух величин путем замены по какой-либо из двух схем:

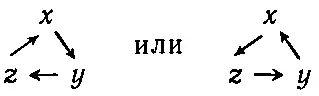
Теперь Мик подсчитывает моменты сил в своей системе.

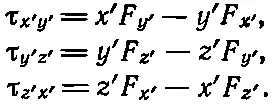(20.2)

Пусть одна система координат повернута на угол θ по отношению к другой, так что ось z осталась той же самой. (Угол θ ничего не имеет общего с вращением объекта или с чем-то происходящим внутри системы координат. Это просто связь между осями, используемыми одним человеком, и осями, используемыми другим. Мы предполагаем, что он остается постоянным.) При этом координаты в двух системах связаны так:

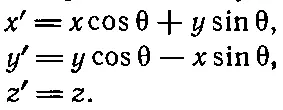(20.3)

Точно таким же образом, поскольку сила является вектором, она преобразуется в новой системе координат так же, как x, y и z. Просто, по определению, объект называется вектором тогда и только тогда, когда различные его компоненты преобразуются как x, y и z

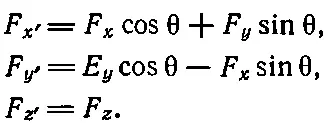(20.4)

Теперь можно определить, как преобразуется момент силы. Для этого в уравнение (20.2) нужно просто подставить вместо х ', у ' и z ' выражение (20.3), а для F x ', F y ', и F z '-— выражение (20.4). В результате для τ x'y'получается длинный ряд членов, но оказывается (и на первый взгляд это удивительно), что все сводится просто к выражению xF y - yF x , которое, как известно, является моментом силы в плоскости ху :

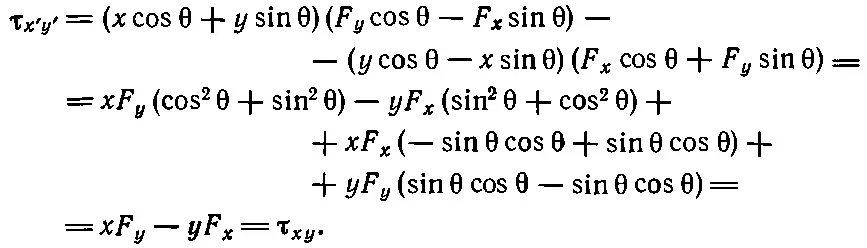(20.5)

Результат совершенно ясен: ведь мы только повернули оси, лежащие в плоскости ху , при этом момент относительно оси z в этой плоскости не отличается от прежнего: ведь плоскость-то осталась той же самой! Более интересно выражение для τ V ' Z '. Здесь уже мы имеем дело с новой плоскостью. Если теперь повторить то же самое с плоскостью y ' z ', то получим

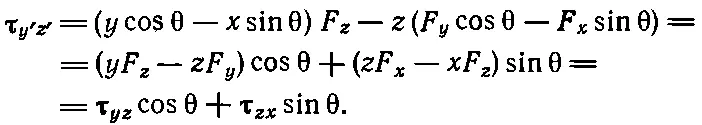(20.6)

И наконец, для плоскости z ' x '

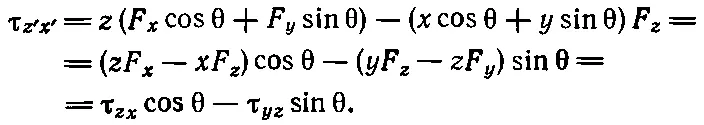(20.7)

Мы хотели найти правило для определения момента сил в новой системе через момент сил в старой и нашли его. Как можно запомнить это правило? Если внимательно посмотреть на уравнения (20.5)—(20.7), то нетрудно увидеть, что между ними и уравнениями для x, y и z существует тесная связь. Если каким-то образом мы бы могли назвать τ xу z-компонентой чего-то, скажем z-компонентой вектора τ, то все было бы в порядке: уравнение (20.5) мы бы понимали как преобразование вектора τ, ибо z-компонента его, как это и должно быть, оставалась бы неизменной. Аналогично, если связать плоскость yz с x- ком понентой новоиспеченного вектора, а плоскость zx с у - компо нентой, то закон преобразования будет выглядеть так: