Ричард Фейнман - Том 1. Механика, излучение и теплота
- Название:Том 1. Механика, излучение и теплота
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 1. Механика, излучение и теплота краткое содержание
Том 1. Механика, излучение и теплота - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Перейдем теперь к формулам и покажем, как кориолисова сила работает на практике. Пусть Мик сидит на карусели, которая кажется ему неподвижной. С точки зрения Джо, который стоит на земле и знает истинные законы механики, карусель крутится. Предположим, что мы провели радиальную прямую на карусели и пусть Мик двигает прямо по этой линии какую-то массу. Я хочу показать, что для того, чтобы все было так, как мы описали, необходима боковая сила. Это можно увидеть, обратив внимание на момент количества движения вращающейся массы. Она крутится все время с одной и той же угловой скоростью ω, поэтому ее момент количества движения равен
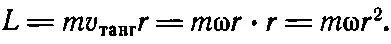
Если масса расположена близко к центру, то он сравнительно мал, но если мы передвигаем ее в новое положение и если мы увеличиваем r, то масса m приобретает больший момент количества движения, т. е. во время движения по радиусу на нее должен действовать некоторый момент силы . (Чтобы на карусели двигаться по радиусу, нужно наклониться и толкаться вбок. Попробуйте как-нибудь сами проделать это.) Поскольку момент силы равен скорости изменения L во время движения массы m по радиусу, то
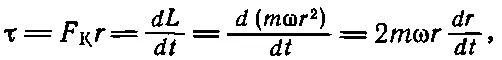
где через F K обозначена сила Кориолиса. В действительности мы хотели узнать, какую боковую силу должен прилагать Мик, чтобы двигать массу m со скоростью v r = dr / dt . Как видите, она равна F K=τ/r=2mωv r.
Теперь, имея формулу для кориолисовой силы, давайте рассмотрим несколько более подробно всю картину в целом. Как можно понять причину возникновения этой силы из элементарных соображений? Заметьте, что кориолисова сила не зависит от расстояния до оси и поэтому действует даже на оси! Оказывается, что легче всего понять именно силу, действующую на оси вращения. Для этого нужно просто посмотреть на все происходящее из инерциальной системы Джо, который стоит на земле. На фиг. 19.4 показаны три последовательных положения массы m, которая при t =0 проходит через ось.
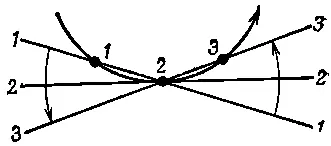
Фиг. 19.4. Три последовательных положения движущейся по радиусу точки вращающегося столика.
Из-за вращения карусели масса, как мы видим, движется не по прямой линии, а по некоторому кривому пути , касающемуся диаметра в точке r=0. Но для того чтобы она двигалась по кривому пути, должна действовать ускоряющая сила. Это и есть кориолисова сила.
Однако с кориолисовой силой мы встречаемся не только в подобных ситуациях. Можно показать, что если предмет движется с постоянной скоростью по краю диска, то на него тоже действует кориолисова сила. Почему? Мик видит предмет движущимся со скоростью v м, а Джо видит его движущимся по окружности со скоростью v д=v м+ωr, поскольку предмет вдобавок переносится каруселью. Как мы уже знаем, действующая в этом случае сила будет, в сущности, полностью центробежной силой скорости v д, равной mv 2 Д / r . Но, с точки зрения Мика, она должна состоять из трех частей. Все это можно записать в следующем виде:
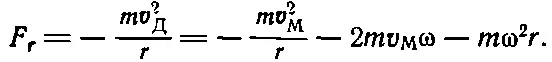
Итак, F r — это сила, которую измеряет Мик. Попытаемся понять, откуда что берется. Может ли Мик признать первый член? «Конечно,— сказал бы он,— даже если бы я не вращался, то такая центробежная сила должна возникнуть, если побежать по кругу со скоростью v м». Итак, это просто центробежная сила, появления которой Мик ожидает и которая не имеет ничего общего с вращением карусели. Вдобавок Мик думает, что должна быть еще одна центробежная сила, действующая даже на неподвижные предметы на его карусели. Это дает третий член. Однако в дополнение к ним существует еще один член — второй, который опять равен 2mωv м. Раньше, при радиальной скорости, кориолисова сила F Kбыла тангенциальна. Теперь же, при тангенциальной скорости, она радиальна. В самом деле, одно выражение отличается от другого только знаком. Сила всегда имеет одно и то же направление по отношению к скорости независимо от того, куда направлена скорость. Она действует под прямым углом к скорости и равна по величине 2mωv.
Глава 20 ВРАЩЕНИЕ В ПРОСТРАНСТВЕ
§ 1. Моменты сил в трехмерном пространстве
В этой главе мы рассмотрим одно из наиболее замечательных и забавных следствий законов механики — поведение крутящегося колеса. Для этого нам прежде всего нужно расширить математическое описание вращения, понятие момента количества движения, момента силы и т. д. на трехмерное пространство. Однако мы не будем использовать эти уравнения во всей их общности и изучать все следствия, ибо это займет многие годы, а нас ждут другие разделы, к которым мы вскоре должны перейти. В вводном курсе можно остановиться только на основных законах и их приложениях к весьма ограниченному числу особенно интересных случаев.
Прежде всего хочу отметить, что для вращения в трех измерениях твердого тела или какого-то иного объекта остается верным все, что мы получили для двух измерений. Иначе говоря, xF y - yF x так и остается моментом силы «в плоскости ху », или моментом силы «относительно оси z». Остается справедливым также, что этот момент силы равен скорости изменения величины хр y - ур x ; если вы вспомните вывод уравнения (18.15) из законов Ньютона, то увидите, что фактически мы не использовали того обстоятельства, что движение плоское, и просто дифференцировали величину хр у - ур x и получали xF y - yF x , так что эта теорема остается верной. Величину хр у - ур x мы называли моментом количества движения в плоскости ху , или моментом количества движения относительно оси z. Кроме плоскости ху , можно использовать другие пары осей и получить другие уравнения. Возьмем, например, плоскость yz . Уже из симметрии ясно, что если мы просто подставим у вместо х , а z вместо у , то для момента силы получим выражение yF z - zF y и yp z - zp y будет угловым моментом в этой плоскости. Разумеется, можно еще взять и плоскость zx и получить для нее
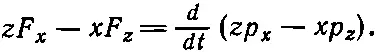
Интервал:
Закладка:




