Ричард Фейнман - Том 1. Механика, излучение и теплота

В этой главе мы вычисляли интенсивность в разных направлениях при различном расположении источников. В заключение выведем формулу, которая нам понадобится в следующей главе, посвященной показателю преломления. До сих пор мы обходились только относительными интенсивностями, а на этот раз мы получим формулу для полной величины поля при условиях, о которых будет рассказано ниже.

Предположим, что имеется некоторая плоскость, которую заполняют осцилляторы, причем все они колеблются в плоскости одновременно, с одной амплитудой и фазой. Чему равно поле на конечном, но достаточно большом расстоянии от плоскости? (Мы не можем выбрать точку наблюдения очень близко от плоскости, потому что у нас нет точных формул для поля вблизи источников.) Пусть плоскость зарядов совпадает с плоскостью XY и нас интересует поле в точке Р, лежащей на оси z, достаточно далеко от плоскости (фиг. 30.10).

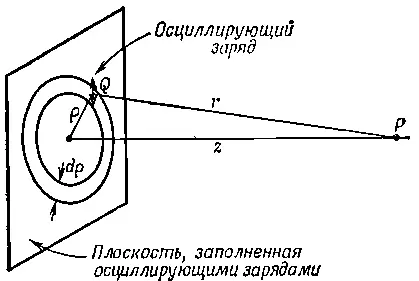
Фиг. 30.10. Поле излучения осциллирующих зарядов, заполняющих плоскость.

Предположим, что число зарядов на единичной площадке равно n, а величина каждого заряда q. Все заряды совершают одинаковые гармонические колебания в одном и том же направлении, с той же амплитудой и фазой. Смещение заряда из его среднего положения описывается функцией x 0cosωt. Вводя комплексную амплитуду, действительная часть которой дает реальное движение, будем описывать колебание заряда функцией x 0e iωt.

Чтобы найти поле, создаваемое всеми зарядами в точке Р, нужно вычислить сначала поле отдельного заряда q, а затем сложить поля всех зарядов. Как известно, поле излучения пропорционально ускорению заряда, т. е.. — ω 2x 0е iωt(и одинаково для всех зарядов). Электрическое поле в точке Р, создаваемое зарядом в точке Q, пропорционально ускорению заряда q, нужно только помнить, что поле в точке Р в момент времени t определяется ускорением заряда в более ранний момент времени t'=t-r/c, где r/c — время, за которое волна проходит расстояние от Q до Р. Поэтому поле в точке Р пропорционально

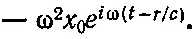(30.10)

Подставляя это значение ускорения в формулу для поля, создаваемого зарядом на большом расстоянии, получаем

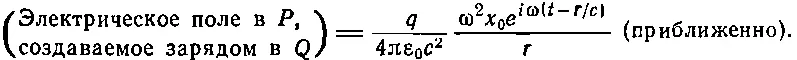(30.11)

Однако эта формула не совсем правильна, поскольку нужно брать не все ускорение целиком, а его компоненту , перпендикулярную линии QP. Мы предположим, однако, что точка Р находится от плоскости намного дальше, чем точка Q от оси z (расстояние ρ на фиг. 30.10), так что для эффектов, которые мы хотим учесть, косинус можно заменить единицей (косинус и так довольно близок к единице).

Полное поле в точке Р получается суммированием вкладов от всех зарядов в плоскости. Разумеется, мы должны взять векторную сумму полей. Но поскольку направление поля примерно одинаково для всех зарядов, в рамках сделанного приближения достаточно сложить величины всех полей. Кроме того, в нашем приближении поле в точке Р зависит только от r, следовательно, все заряды с одинаковым r создают равные поля. Поэтому, прежде всего, сложим поля всех зарядов в кольце шириной dρ и радиусом ρ. Интегрируя затем по всем ρ, получаем полное поле всех зарядов.

Число зарядов в кольце равно произведению площади кольца, 2πρdρ, на η — плотность зарядов на единицу площади. Отсюда

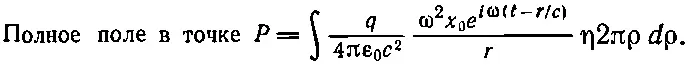
Интеграл берется в пределах ρ=0 и ρ=∞. Время t , конечно, зафиксировано, так что единственными меняющимися величинами являются ρ и r. Отвлечемся пока от постоянных множителей, включая и e i ω t , и вычислим интеграл

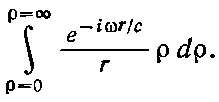(30.13)

Для этого учтем соотношение между ρ и r:

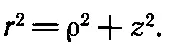(30.14)

При дифференцировании формулы (30.14) z нужно считать независимым от ρ, тогда

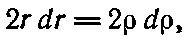
что очень кстати, поскольку при замене в интеграле ρdρ на r dr знаменатель r сокращается. Интеграл приобретает более простой вид

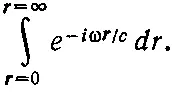(30.15)

Экспонента интегрируется очень просто. Нужно поставить в знаменатель коэффициент при r в показателе экспоненты и взять саму экспоненту в точках, соответствующих пределам. Но пределы по r отличаются от пределов по ρ. Когда ρ=0, нижний предел r=z, т. е. пределы по r равны z и бесконечности. Интеграл (30.15) равен

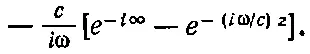(30.16)

Вместо (r/с)∞ мы здесь написали ∞, поскольку и то и другое означает просто сколь угодно большую величину!

А вот е - i ∞— величина загадочная. Ее действительная часть, равная cos(-∞), с математической точки зрения величина совершенно неопределенная. [Хотя можно допустить, что она находится где-то [а может быть и всюду (?)—между +1 и -1!]Но в физической ситуации эта величина может означать нечто вполне разумное и обычно оказывается равной нулю. Чтобы убедиться, что это так в нашем случае, вернемся к первоначальному интегралу (30.15)

Выражение (30.15) можно понимать как сумму большого числа маленьких комплексных чисел, модуль которых Δr, а угол в комплексной плоскости θ=-ωr/с. Попробуем оценить эту сумму графически. На фиг. 30.11 отложены первые пять членов суммы. Каждый отрезок кривой имеет длину Δr и расположен под углом Δθ=-ω(Δr/ с ) к предыдущему отрезку. Сумма первых пяти слагаемых обозначена стрелкой из начальной точки к концу пятого отрезка. Продолжая прибавлять отрезки, мы опишем многоугольник, вернемся примерно к начальной точке и начнем описывать новый многоугольник. Чем большее число отрезков мы будем прибавлять, тем большее число раз мы обернемся, двигаясь почти по окружности с радиусом с/. Теперь понятно, почему интеграл дает при вычислении неопределенный ответ!