Ричард Фейнман - Том 1. Механика, излучение и теплота

Вычислим теперь полную энергию, излучаемую зарядом при ускорении. Для общности возьмем случай произвольного ускорения, считая, однако, движение нерелятивистским. Когда ускорение направлено, скажем, по вертикали, электрическое поле излучения равно произведению заряда на проекцию запаздывающего ускорения, деленному на расстояние. Таким образом, нам известно электрическое поле в любой точке, а отсюда мы знаем энергию ε 0cE 2, проходящую через единичную площадку за 1 сек.

Величина ε 0c часто встречается в формулах распространения радиоволн. Обратную ей величину можно назвать импедансом вакуума (или сопротивлением вакуума); она равна 1/ε 0с=377 ом. Отсюда мощность (в ваттах на квадратный метр) есть средний квадрат поля, деленный на 377.

С помощью формулы (29.1) для электрического поля мы получаем

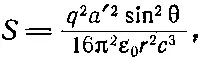(32.2)

где S — мощность на 1 м 2, излучаемая под углом θ. Как уже отмечалось, S обратно пропорционально расстоянию. Интегрируя, получаем отсюда полную мощность, излучаемую во всех направлениях. Для этого сначала умножим S на площадь полоски сферы, тогда мы получим поток энергии в интервале угла dθ (фиг. 32.1).

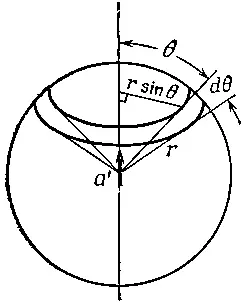
Фиг. 32.1. Площадь кольца на сфере, равная 2πr 2 sinθrdθ.

Площадь полоски вычисляется следующим образом: если радиус равен r, то толщина полоски равна rdθ, а длина 2πrsinθ, поскольку радиус кольцевой полоски есть rsinθ. Таким образом, площадь полоски равна

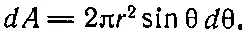(32.3)

Умножая поток [мощность на 1 м 2, согласно формуле (32.2)] на площадь полоски, найдем энергию, излучаемую в интервале углов θ и θ+dθ; далее нужно проинтегрировать по всем углам θ от 0 до 180°:

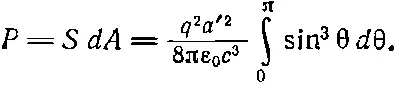(32.4)

При вычислении 0∫ πsin 3θdθ воспользуемся равенством sin 3θ=(1—cos 2θ) sinθ и в результате получим 4/3. Отсюда окончательно

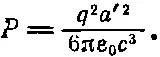(32.5)

Необходимо сделать несколько замечаний по поводу этого выражения. Прежде всего, поскольку а' есть вектор, то а' 2в формуле (32.5) означает а'· а', т. е. квадрат длины вектора. Во-вторых, в формулу (32.2) для потока входит ускорение, взятое с учетом запаздывания, т. е. ускорение в тот момент времени, когда была излучена энергия, проходящая сейчас через поверхность сферы. Может возникнуть мысль, что энергия действительно была излучена точно в указанный момент времени. Но это не совсем правильно. Момент излучения нельзя определить точно. Можно вычислить результат только такого движения, например колебания и т. п., где ускорение в конце концов исчезает. Следовательно, мы можем найти только полный поток энергии за весь период колебаний, пропорциональный среднему за период квадрату ускорения. Поэтому а' 2в (32.5) должно означать среднее по времени от квадрата ускорения. Для такого движения, когда ускорение в начале и в конце обращается в нуль, полная излученная энергия равна интегралу по времени от выражения (32.5).

Посмотрим, что дает формула (32.5) для осциллирующей системы, для которой ускорение а' имеет вид -ω 2x 0е iωt. Среднее за период от квадрата ускорения равно (при возведении в квадрат надо помнить, что на самом деле вместо экспоненты должна входить ее действительная часть — косинус, а среднее от cos 2ωt дает 1/ 2):

Следовательно,

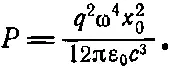(32.6)

Эти формулы были получены сравнительно недавно — в начале XX века. Это замечательные формулы, они имели огромное историческое значение, и о них стоило бы почитать в старых книгах по физике. Правда, там использовалась другая система единиц, а не система СИ. Однако в конечных результатах, относящихся к электронам, эти осложнения можно исключить с помощью следующего правила соответствия: величина q e 2/4πε 0, где q е— заряд электрона (в кулонах), раньше записывалась как е 2. Легко убедиться, что в системе СИ значение е численно равно 1,5188·10 -14, поскольку мы знаем, что q e=1,60206·10 -19и 1/4πε 0=8,98748·10 9. В дальнейшем мы будем часто пользоваться удобным обозначением

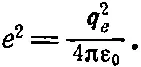(32.7)

Если это численное значение e подставить в старые формулы, то все остальные величины в них можно считать определенными в системе СИ. Например, формула (32.5) прежде имела вид Р = 2/ 3е 2а 2/с 3. А потенциальная энергия протона и электрона на расстоянии r есть q e 2/4πε 0r или е 2/r, где е =1,5188·10 -14ед. СИ.

Заряд, закрепленный на пружине с собственной частотой ω 0(или электрон в атоме), даже в абсолютно пустом пространстве не сможет колебаться бесконечно долго, поскольку, колеблясь, он теряет энергию на излучение. Никаких сил сопротивления в обычном смысле этого слова, никакой вязкости здесь нет. Но колебания не будут происходить «вечно», вследствие излучения они будут медленно замирать. А насколько медленно? Определим для осциллятора величину Q , вызванную так называемым радиационным сопротивлением или радиационным затуханием. Для любой колеблющейся системы величина Q равна энергии системы в данный момент времени, деленной на потери энергии, отнесенные к 1 рад :

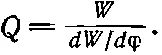
Запишем Q по-другому, пользуясь для этого равенством dW/dφ=(dW/dt)/(dφ /dt)=-(dW/dt)/ω:

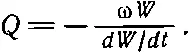
Если Q задано, то легко получить закон спадания энергии колебаний: dW/dt=(-ω/Q)W, откуда следует W=W 0e -ωt/Q; здесь W 0— начальная энергия (при t=0).

Чтобы найти Q для излучающего осциллятора, вернемся к формуле (32.8) и подставим вместо dW/dt выражение (32.6).

А что нужно взять в качестве энергии W осциллятора? Кинетическая энергия осциллятора равна 1/2mv 2, а средняя кинетическая энергия равна mω 2x 0 2/4. Но мы помним, что полная энергия осциллятора равна средней кинетической плюс средняя потенциальная, причем обе они для осциллятора равны; поэтому полная энергия равна