Ричард Фейнман - Том 1. Механика, излучение и теплота

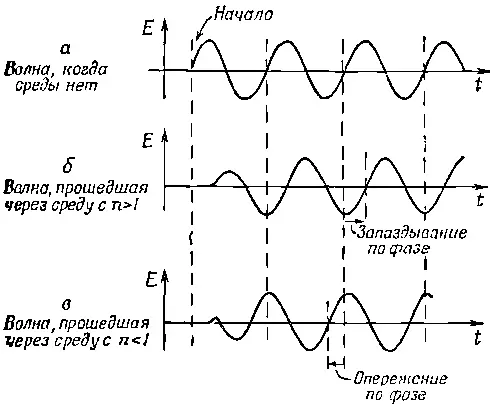
Фиг. 31.4. Волновые «сигналы».

Из рисунка видно, что для волны, проходящей в среде с опережением по фазе, сигнал (т. е. начало волны) не опережает по времени сигнал источника.

Обратимся теперь снова к дисперсионной формуле. Следует помнить, что полученный нами результат несколько упрощает истинную картину явления. Чтобы быть точными, в формулу необходимо внести некоторые поправки. Прежде всего в нашу модель атомного осциллятора следует ввести затухание (иначе осциллятор, раз начав, будет колебаться до бесконечности, что неправдоподобно). Движение затухающего осциллятора мы уже изучали в одной из прошлых глав [см. уравнение (23.8)]. Учет затухания приводит к тому, что в формулах (31.16), а поэтому и в (31.19), вместо (ω 0 2-ω 2) появляется (ω 0 2-ω 2+iγω), где γ — коэффициент затухания.

Вторая поправка к нашей формуле возникает потому, что каждый атом обычно имеет несколько резонансных частот. Тогда вместо одного вида осцилляторов, нужно учесть действие нескольких осцилляторов с разными резонансными частотами, колебания которых происходят независимо друг от друга, и сложить вклады от всех осцилляторов.

Пусть в единице объема содержится N kэлектронов с собственной частотой (ω kи коэффициентом затухания γ k. Наша дисперсионная формула примет в результате вид

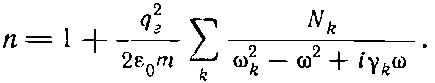(31.20)

Это окончательное выражение для показателя преломления справедливо для большого числа веществ [23] Такая же формула получается и с помощью квантовой механики, однако интерпретация ее в этом случае иная. В квантовой механике даже одноэлектронный атом, например водород, имеет несколько резонансных частот. Поэтому вместо числа электронов N k с частотой ω k появляется множитель Nf k где N — число атомов в единице объема, а число f k (называемое силой осциллятора) указывает, с каким весом входит данная резонансная частота ω k . . Примерный ход показателя преломления с частотой, даваемый формулой (31.20), приведен на фиг. 31.5.

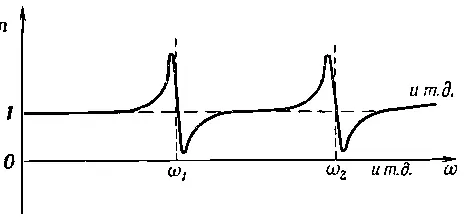
Фиг. 31.5. Показатель преломления как функция частоты.

Вы видите, что всюду, за исключением области, где ω очень близко к одной из резонансных частот, наклон кривой положителен. Такая зависимость носит название «нормальной» дисперсии (потому что этот случай встречается наиболее часто). Вблизи резонансных частот кривая имеет отрицательный наклон, и в этом случае говорят об «аномальной» дисперсии (имея в виду «ненормальную» дисперсию), потому что она была наблюдена задолго до того, как узнали об электронах, и казалась в то время необычной. С нашей точки зрения, оба наклона вполне «нормальны»!

Вы уже, наверное, заметили нечто странное в последней форме (31.20) нашей дисперсионной формулы. Из-за члена iγ, учитывающего затухание, показатель преломления стал комплексной величиной! Что это означает? Выразим n через действительную и мнимую части:

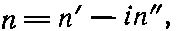(31.21)

причем n' и n" вещественны. (Перед in" стоит знак минус, а само n", как легко убедиться, положительно.)

Смысл комплексного показателя преломления легче всего понять, вернувшись к уравнению (31.6) для волны, проходящей сквозь пластинку с показателем преломления n. Подставив сюда комплексное n и произведя перегруппировку членов, получаем

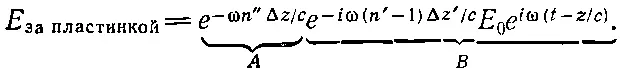(31.22)

Множители, обозначенные буквой В, имеют прежний вид и, как и раньше, описывают волну, фаза которой после прохождения пластинки запаздывает на угол ω( n '-1)Δ z / c . Множитель А (экспонента с действительным показателем) представляет нечто новое. Показатель экспоненты отрицателен, следовательно, А вещественно и меньше единицы. Множитель А уменьшает амплитуду поля; с ростом Δz величина А, а следовательно, и вся амплитуда падает. При прохождении через среду электромагнитная волна затухает. Среда «поглощает» часть волны. Волна выходит из среды, потеряв часть своей энергии. Этому не следует удивляться, потому что введенное нами затухание осцилляторов обусловлено силой трения и непременно приводит к потере энергии. Мы видим, что мнимая часть комплексного показателя преломления n" описывает поглощение (или «ослабление») электромагнитной волны. Иногда n" называют еще «коэффициентом поглощения».

Заметим также, что появление мнимой части n отклоняет стрелку, изображающую Е ана фиг. 31.3, к началу координат.

Отсюда ясно, почему поле ослабевает при прохождении через среду.

Обычно (как, например, у стекла) поглощение света очень мало. Именно так и получается по нашей формуле (31.20), потому что мнимая часть знаменателя iγ kω много меньше действительной части (ω k 2-ω 2). Однако когда частота ω близка к ω k, резонансный член (ω k 2-ω 2) оказывается мал по сравнению с iγ kω и показатель преломления становится почти чисто мнимым. Поглощение в этом случае определяет основной эффект. Именно поглощение дает в солнечном спектре темные линии. Свет, излучаемый поверхностью Солнца, проходит сквозь солнечную атмосферу (а также через атмосферу Земли), и частоты, равные резонансным частотам атомов в атмосфере Солнца, сильно поглощаются.

Наблюдение подобных спектральных линий солнечного света позволяет установить резонансные частоты атомов, а следовательно, и химический состав солнечной атмосферы. Точно так же по спектру звезд узнают состав звездного вещества. С помощью этих методов обнаружили, что химические элементы на Солнце и звездах не отличаются от земных.

Как мы видели, мнимая часть показателя преломления характеризует поглощение. Попробуем теперь вычислить энергию, переносимую световой волной. Мы высказали соображения в пользу того, что энергия световой волны пропорциональна —Е 2, среднему по времени от квадрата электрического поля волны. Ослабление электрического поля за счет поглощения волны должно приводить к потере энергии, переходящей в какое-то трение электронов и в конечном счете, как нетрудно догадаться, в тепло.

Взяв часть световой волны, падающую на единичную площадку, например на квадратный сантиметр поверхности нашей пластинки на фиг. 31.1, можно записать энергетический баланс в следующей форме (мы предполагаем, что энергия сохраняется!):