Ричард Фейнман - Том 1. Механика, излучение и теплота

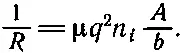(43.20)

Мы нашли связь сопротивления со свойствами молекул n i q и μ, которое в свою очередь зависит от τ и m. Если мы при помощи атомных измерений определим n iи q, то, измеряя R , можно определить μ, а потом и τ.

Перейдем к другой задаче, для которой нам придется несколько изменить метод анализа, — к задаче о диффузии. Предположим, что мы взяли ящик, заполненный газом, находящимся в тепловом равновесии, а потом в любое место внутри ящика вспрыснули небольшое количество другого газа. Назовем первоначальный газ газом «фона», а новый газ — «особым» газом. Особый газ начинает распространяться по всему ящику, но распространение это замедляется наличием молекул фона. Явление такого замедленного распространения называется диффузией . Диффузия в основном определяется столкновениями молекул особого газа с молекулами фона. После многих столкновений особые молекулы более или менее равномерно распределятся по всему ящику. Важно не спутать диффузию газа с переносом больших количеств вещества в результате конвекционных токов. Обычно смешение двух газов происходит именно в результате комбинации конвекции и диффузии. Сейчас нас интересует только такое перемешивание, которое не сопровождается « порывами ветра ». Газ распространяется только благодаря молекулярному движению, т. е. происходит диффузия. Давайте выясним, быстро ли происходит диффузия.

Итак, мы приступаем к вычислению общего потока молекул особого газа, порождаемого молекулярным движением. Общий поток не равен нулю только тогда, когда распределение молекул отличается от равновесного, иначе усреднение молекулярного движения сводит общий поток к нулю. Рассмотрим сначала поток в направлении оси х . Чтобы определить, чему этот поток равен, мы должны вообразить площадку, перпендикулярную к оси, и подсчитать число молекул, пересекающих эту площадку. Чтобы определить общий поток, мы должны считать положительными те молекулы, которые движутся в направлении положительных x, и вычесть из этого числа те молекулы, которые движутся в противоположном направлении. Как мы неоднократно убеждались, число молекул, пересекающих площадку в течение времени Δ T , равно числу молекул, находящихся к началу интервала Δ T внутри объема, заключенного между нашей площадкой и площадкой, расположенной от нее на расстоянии v Δ T . (Заметим, что здесь v — настоящая скорость молекулы, а отнюдь не скорость дрейфа.)

Мы упростим наши выкладки, если возьмем площадку единичной площади. Тогда число особых молекул, пересекающих площадку слева направо (справа от площадки лежат положительные x-направления), равно n - v Δ T , где n -— число особых молекул в единичном объеме слева от площадки (с точностью до множителя ~ 1/ 6, но мы такими множителями пренебрежем!). Аналогично, число особых молекул, движущихся справа налево, равно n + v Δ T , где n +— плотность особых молекул справа от площадки. Если мы обозначим молекулярный поток буквой J, под которой мы будем понимать общий поток молекул через единичную площадку за единицу времени, то получим

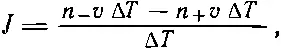(43.21)

или

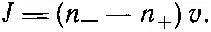(43.22)

А что понимать под n -и n +? Когда мы говорим «плотность слева от площадки», то как далеко налево? Мы должны измерить плотность в том месте, откуда молекула отправляется в свой «свободный полет», потому что число стартующих молекул определяется числом молекул, находящихся в этом месте. Таким образом, n -— это плотность молекул на расстоянии длины свободного пробега l слева от нашей воображаемой площадки, а n +— плотность молекул на расстоянии длины свободного пробега справа от нее.

Распределение особых молекул в ящике удобно описывать с помощью непрерывной функции x, y и z , которую мы обозначим n a. Под n a( x, y, z ) нужно понимать плотность особых молекул в маленьком объеме вокруг точки ( x, y, z ). Тогда разность ( n +- n -) можно представить в виде

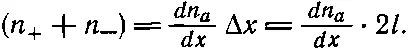(43.23)

Подставляя этот результат в (43.22) и пренебрегая множителем 2, получаем

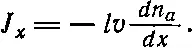(43.24)

Мы выяснили, что поток особых молекул пропорционален производной плотности, или, как иногда говорят, «градиенту плотности».

Ясно, что мы сделали несколько грубых приближений. Не говоря уже о том, что мы постоянно забывали о множителях, мы использовали v , когда нужно было ставить v x , а разместив объемы, содержащие молекулы n +и n -, на концах перпендикуляров к площадке, взяли перпендикуляры длиной l . Между тем для тех молекул, которые движутся не перпендикулярно к поверхности, l соответствует длине наклонного пути. Можно исправить эти недоделки; более тщательный анализ показал бы, что правую часть уравнения (43.24) нужно умножить на 1/ 3. Итак, более правильный ответ выглядит следующим образом:

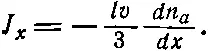(43.25)

Аналогичные уравнения можно написать для токов вдоль y - и z-направлений.

С помощью макроскопических наблюдений можно измерить ток J x и градиент плотности dn a / dx . Их отношение, найденное экспериментально, называется «коэффициентом диффузии» D . Это значит, что

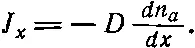(43.26)

Мы смогли показать, что ожидаемое значение коэффициента D для газа равно

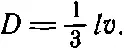(43.27)

Пока мы изучили в этой главе два разных процесса: подвижность (дрейф молекул под действием «внешней» силы) и диффузию (разбегание молекул, определяемое только внутренними силами, случайными столкновениями). Однако эти процессы связаны друг с другом, потому что в основе обоих явлений лежит тепловое движение, и оба раза в расчетах появлялась длина свободного пробега l .