Ричард Фейнман - Том 1. Механика, излучение и теплота

Если в уравнение (43.25) подставить l = v τ и τ=μm, то получится

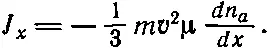(43.28)

Ho mv 2зависит только от температуры. Мы еще помним, что

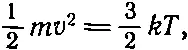(43.29)

так что

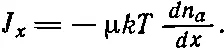(43.30)

Таким образом, D , коэффициент диффузии , равен произведению kT на μ, коэффициент подвижности :

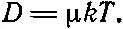(43.31)

Оказывается, что (43.31) — это точное соотношение между коэффициентами. Хотя мы исходили из очень грубых предположений, не нужно к нему добавлять никаких дополнительных множителей. Можно показать, что (43.31) в самом деле всегда удовлетворяется точно. Это верно даже в очень сложных случаях (например, для случая взвешенных в жидкости мелких частиц), когда наши простые вычисления явно отказываются служить.

Чтобы показать, что (43.31) верно в самых общих случаях, мы выведем его иначе, используя только основные принципы статистической механики. Представьте себе, что почему-то существует градиент «особых» молекул и возник ток диффузии, пропорциональный, согласно (43.26), градиенту плотности. Тогда мы создадим в направлении оси х силовое поле так, что на каждую особую молекулу будет действовать сила F . По определению подвижности μ скорость дрейфа дается соотношением

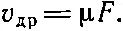(43.32)

Используя обычные аргументы, можно найти ток дрейфа ( общее число молекул, пересекающих единичную площадку за единицу времени):

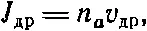(43.33)

или

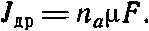(43.34)

А теперь можно так распорядиться силой F , что ток дрейфа, вызываемый силой F, скомпенсирует диффузию, тогда полный ток особых молекул будет равен нулю. В этом случае мы имеем J x+J др=0, или

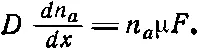(43.35)

В этом случае «компенсации» существует постоянный (во времени) градиент плотности, равный

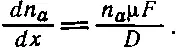(43.36)

Теперь уже легко соображать дальше! Ведь мы добились равновесия и можем теперь применять наши равновесные законы статистической механики. По этим законам вероятность найти молекулу около точки х пропорциональна ехр(- U / kT ), где U — потенциальная энергия. Если говорить о плотности молекул n а , то это значит:

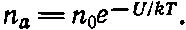(43.37)

Дифференцируя (43.37) по х , получаем

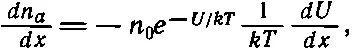(43.38)

или

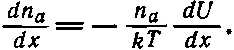(43.39)

В нашем случае сила F направлена вдоль оси х и потенциальная энергия U равна - Fx , а - dU / dx = F . Уравнение (43.39) принимает вид

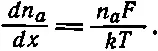(43.40)

[Это в точности уравнение (40.2), из которого мы и вывели ехр(- U / kT ); круг замкнулся.] Сравнивая (43.40) и (43.36), мы получаем уравнение (43.31). Мы показали, что в уравнении (43.31), которое выражает ток диффузии через подвижность, все коэффициенты правильны, а само уравнение правильно всегда. Подвижность и диффузия тесно связаны. Эту связь открыл Эйнштейн.

Методы кинетической теории, которую мы так успешно применяли, позволяют также рассчитать и теплопроводность газа. Если газ в верхней части ящика горячее, чем внизу, то тепло перетечет сверху вниз. (Мы предполагаем, что теплее верхняя часть ящика, потому что в противном случае возникнут поднимающиеся вверх конвекционные токи, а этот случай уже не имеет отношения к теплопроводности .) Перенос тепла от горячего газа к холодному вызывается диффузией «горячих» молекул (т. е. молекул с большой энергией) вниз и диффузией «холодных» молекул вверх. Чтобы вычислить поток тепловой энергии, мы должны узнать сначала об энергии, переносимой через выделенную площадку сверху вниз (ее переносят движущиеся вниз молекулы), потом об энергии, переносимой через эту же площадку снизу вверх (за это уже отвечают молекулы, поднимающиеся вверх). Разность этих потоков энергии даст нам полный поток энергии сверху вниз.

Теплопроводность ϰ определяется как отношение скорости переноса тепловой энергии через единичную площадку к градиенту температуры:

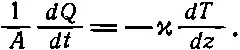(43.41)

Поскольку ход вычислений теплопроводности очень похож на вычисление потока заряженных частиц в ионизованном газе, то мы предлагаем читателю в виде упражнения доказать, что

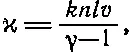(43.42)

при этом (γ-1) kT —средняя энергия молекулы при температуре Т .

Если вспомнить о соотношении nl σ c =1, то теплопроводность можно записать в виде

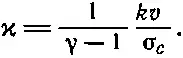(43.43)

Мы получили поистине удивительный результат. Известно, что средняя скорость молекул газа зависит от температуры и не зависит от плотности . Можно думать, что σ с зависит только от размеров молекул. Таким образом, наш очень простой вывод сводится к тому, что теплопроводность ϰ (а следовательно, и скорость потока тепла в каждом частном случае) не зависит от плотности газа! Изменение числа «носителей» энергии при изменениях плотности в точности компенсируется изменением расстояния, которое пробегает «носитель» между столкновениями.