Ричард Фейнман - Том 1. Механика, излучение и теплота

Сейчас приступим к выводам. В механике мы подошли ко всем нужным нам результатам, исходя из центра механического мира F=m a. Такую же роль в термодинамике сыграет только что найденный нами принцип. Но какие выводы можно сделать, исходя из этого принципа?

Ну начнем. Сначала скомбинируем закон сохранения энергии и закон, связывающий Q 1и Q 2, чтобы найти коэффициент полезного действия обратимой машины . Первый закон говорит, что W = Q 1- Q 2. Согласно нашему новому принципу,

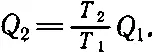
Поэтому работа равна

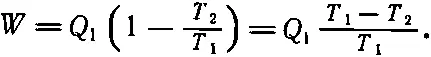(44.13)

Это соотношение характеризует эффективность машины, т. е. количество работы, произведенное при заданной затрате тепла. Коэффициент полезного действия пропорционален перепаду температур, при котором работает машина, деленному на более высокую температуру:

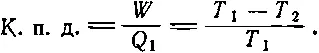(44.14)

Коэффициент полезного действия не может быть больше единицы, а абсолютная температура не может быть меньше нуля, абсолютного нуля. Таким образом, раз T 2должна быть положительной, то коэффициент полезного действия всегда меньше единицы. Это наш первый вывод.

Уравнение (44.7) или (44.12) может быть истолковано особо. При работе обратимых машин Q 1/ T 1= Q 2/ T 2, и тепло Q 1при температуре Т 1«эквивалентно» теплу Q 2при температуре T 2; ведь если поглощается Q 1, то всегда выделяется тепло Q 2. Если теперь придумать для Q / T особое название, то можно сказать, что при обратимых процессах поглощается столько же Q / T , сколько и выделяется. Иначе говоря, Q / T не убывает и не прибывает. Эта величина Q / T называется энтропией , и мы говорим, что «за обратимый цикл изменение энтропии равно нулю». Если T=1°, то энтропия равна Q/1°; мы уже снабдили энтропию особым символом S = Q S /1°. Энтропия повсюду обозначается буквой S , а численно она равна теплу (которое мы обозначили буквой Q S ), выделяемому в одноградусном резервуаре (энтропия не равна просто теплу, это тепло, деленное на температуру, и измеряется она в джоулях на градус ).

Интересно, что, кроме давления, которое зависит от температуры и объема, и внутренней энергии (функции все тех же объема и температуры), мы нашли еще величину — энтропию вещества, которая тоже является функцией состояния. Постараемся объяснить, как вычислять энтропию и что мы понимаем под словами «функция состояния». Проследим за поведением системы в разных условиях. Мы уже умеем создавать разные условия экспериментально, например можно заставить систему расширяться адиабатически или изотермически. (Между прочим, машина не обязательно должна иметь только два резервуара, может быть и три, и четыре различные температуры, и машина будет обмениваться теплом с каждым из резервуаров.) Мы можем прогуляться по всей диаграмме pV , переходя от одного состояния к другому. Иначе говоря, можно перевести газ из состояния а в какое-нибудь другое состояние b и потребовать, чтобы переход из а в b был обратимым. Теперь предположим, что вдоль пути из а в b поставлены маленькие резервуары с разными температурами. Тогда каждый короткий шажок будет сопровождаться изъятием из вещества тепла dQ и передачей его в резервуар при температуре, соответствующей данной точке пути. Давайте свяжем все эти резервуары с помощью обратимых тепловых машин с одним резервуаром единичной температуры. После того как мы закончим перевод вещества из состояния а в состояние b , мы вернем все резервуары в их первоначальное состояние. Обратимая машина вернет каждую дольку тепла dQ , изъятого из вещества при температуре Т , и каждый раз при единичной температуре будет выделяться энтропия dS , равная

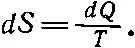(44.15)

Подсчитаем полное количество выделенной энтропии. Разность энтропии, или энтропия, нужная для перехода из а в b в результате какого-нибудь обратимого изменения, это — полная энтропия, т. е. энтропия, взятая из маленьких резервуаров и выделенная при единичной температуре:

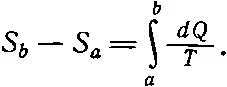(44.16)

Вопрос заключается в том, зависит ли разность энтропии от пути в плоскости pV? Из а в b ведет много дорог. Вспомним, что в цикле Карно мы могли перейти из точки а в точку с (см. фиг. 44.6) двумя способами. Можно было расширить газ сначала изотермически, а потом адиабатически, а можно было начать с адиабатического расширения и окончить изотермическим. Итак, мы должны выяснить, меняется ли энтропия при изменении пути из а в b (фиг. 44.10).

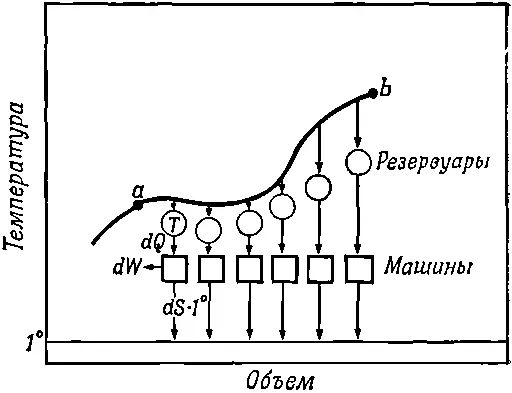
Фиг. 44.10. Изменение энтропии при обратимом переходе.

Она не должна измениться , потому что если мы совершим полный цикл, выйдя из а в b по одному пути и возвратясь по другому, то это путешествие будет эквивалентно полному циклу обратимой машины. При таком цикле никакого тепла не передается одноградусному резервуару.

Поскольку мы не имеем права взять тепло из одноградусного резервуара, то при каждом путешествии из а в b приходится обходиться одним и тем же количеством энтропии. Это количество не зависит от пути , существенны только конечные точки. Таким образом, можно говорить о некоторой функции, которую мы назвали энтропией вещества. Эта функция зависит только от состояния вещества, т. е. только от объема и температуры.

Можно найти функцию S ( V,Т ). Мы подсчитаем изменение энтропии при обратимых изменениях вещества, следя за теплом, выделяемым в одноградусном резервуаре. Но это изменение можно выразить еще в терминах тепла dQ , изымаемого у вещества при температуре Т :

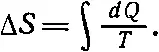(44.17)

Полное изменение энтропии равно разности энтропии в конечной и начальной точках пути: