Ричард Фейнман - Том 1. Механика, излучение и теплота

Чтобы лучше понять, что происходит, нарисуем кривую зависимости давления газа от его объема (фиг. 44.6).

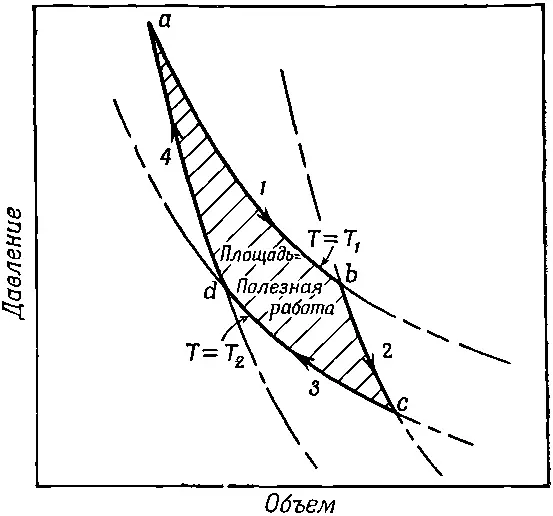
Фиг. 44.6. Цикл Карно.

Когда газ расширяется, его давление падает. Кривая 1 показывает, как изменяются объем и давление, если в цилиндре поддерживается постоянная температура Т 1. Для идеального газа эта кривая описывается уравнением PV = NkT 1. Во время изотермического расширения по мере увеличения объема давление падает, пока мы не остановимся в точке b. За это время газ заберет из резервуара тепло Q 1; ведь мы уже знаем, что если бы газ расширялся, не соприкасаясь с резервуаром, он бы остыл. Итак, мы закончили расширение в точке b . Давайте теперь снимем цилиндр с резервуара и продолжим расширение. Но теперь теплу уже неоткуда взяться. И снова мы медленно выдвигаем поршень, так что нет причины, почему бы процесс мог быть необратимым. Конечно, мы опять предполагаем, что трения нет. Газ продолжает расширяться, и температура падает, потому что связь с источниками тепла прервана.

Будем расширять газ так, чтобы расширение описывалось кривой 2 до тех пор, пока мы не достигнем точки с , где температура упадет до T 2. Такое расширение без притока тепла называется адиабатическим . Мы уже знаем, что в случае идеального газа кривая 2 имеет вид PV γ=const, где γ — постоянная, большая единицы; поэтому адиабатическая кривая падает круче изотермической. Если температура газа в цилиндре достигла Т 2, то, положив цилиндр на вторую тепловую подушку, мы не рискуем вызвать температурных изменений.

Теперь можно медленно сжать газ, продвигаясь по кривой 3, причем цилиндр соприкасается с резервуаром при температуре T 2(см. фиг. 44.5, шаг 2). Поскольку цилиндр соприкасается с резервуаром, его температура не может повыситься, но газу придется отдать резервуару тепло Q 2при температуре T 2. Продвинувшись по кривой 3 до точки d , мы снова снимем цилиндр с тепловой подушки при температуре Т 2и продолжаем сжимать газ. На этот раз мы не станем отбирать у газа тепло. При этом поднимется температура, а давление пойдет по кривой 4. Если мы тщательно проделаем все этапы, то вернемся к исходной точке а при температуре Т 1и можем повторить цикл.

По этой диаграмме судя, газ совершил полный цикл, отняв за это время тепло Q 1при температуре T 1и отдав тепло Q 2при температуре T 2. Этот цикл обратим, и поэтому мы можем шаг за шагом проделать весь путь в обратном направлении. Мы могли бы пойти назад, а не вперед, могли бы начать движение из точки а при температуре T 1, двигаться по кривой 4, затем поглотить тепло Q 2при температуре T 2(для этого надо все время выдвигать поршень) и т. д., пока цикл не будет завершен. Если мы совершали цикл в одном направлении, то заставили газ работать, если же нам захотелось повернуть назад, то придется поработать самим.

Между прочим, легко сосчитать полную работу. Полная работа, совершаемая при расширении, равна произведению давления на изменение объема: ∫ PdV . На нашей диаграмме мы откладывали Р вертикально, а V горизонтально. Если обозначать вертикальное расстояние буквой у , а горизонтальное буквой х , то мы получим интеграл ∫ ydx , а это — площадь под кривой. Таким образом, площадь под каждой из пронумерованных кривых измеряет работу, совершенную либо газом, либо нами за соответствующий этап цикла. Легко понять, что чистый выход работы равен площади внутри кривых.

Раз уж мы привели пример одной обратимой машины, то можно предположить, что возможно существование и других таких же устройств. Пусть обратимая машина А забирает Q 1при T 1совершает работу W и возвращает какое-то количество тепла при температуре Т 2. Предположим, что у нас есть еще одна машина В — творение рук человека, уже сконструированная, а может быть, еще и не изобретенная. Можно взять паровую машину, колесо с резиновыми спицами — словом, что угодно. Мы даже не интересуемся, обратима ли эта машина. Важно только, чтобы она забирала тепло Q 1при температуре Т 1и возвращала часть этого тепла при более низкой температуре Т 2. Предположим, что машина В совершает некую работу W'. Теперь покажем, что W ' не может быть больше W ; нет такой машины, которая работала бы лучше, чем обратимая. Но почему? Предположим, что W ' больше W . Тогда мы можем забрать тепло Q 1при температуре Т 1и отдать его машине В . Эта машина совершит работу W ' и отдаст какое-то количество тепла (неважно какое) резервуару с температурой Т 2. После этого мы можем распорядиться какой-то частью работы W ', которую мы считаем больше W . Прибережем пока часть работы W , а остаток W '- W употребим с пользой для себя (фиг. 44.7).

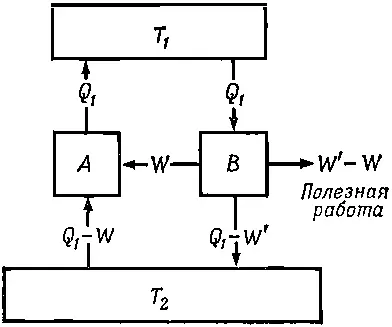
Фиг. 44.7. Машина В заставляет работать обратимую машину А в обратном направлении.

Обладая работой W , можно запустить машину А в обратном направлении, ведь это — обратимая машина . При этом она поглотит какое-то количество тепла из резервуара с температурой Т 2, но зато вернет тепло Q 1резервуару при температуре Т 1. Каков чистый результат этого двойного цикла? Мы вернули все к исходному состоянию и совершили дополнительную работу W '- W . Дело свелось к тому, что мы извлекли энергию из резервуара с температурой Т 2! Тепло Q 1, взятое из резервуара с температурой T 1, было аккуратно возвращено. Раз это тепло все равно возвращается, то в качестве резервуара с температурой Т 1можно взять что-нибудь поменьше океана и заключить это устройство внутрь составной машины А + В . Чистым результатом цикла такой машины будет изъятие из резервуара при температуре Т 2тепла W '- W и превращение его в работу. Но извлечение полезной работы из резервуара при неизменной температуре без других изменений запрещается постулатом Карно. Этого нельзя сделать. Таким образом, не существует таких машин, которые извлекли бы некоторое количество тепла из резервуара при температуре Т 1, возвратили бы какую-то его часть при температуре Т 2и совершили большую работу, чем обратимая машина, работающая при тех же самых температурных условиях.

Предположим теперь, что машина В тоже обратима. Тогда, конечно, не только W ' не больше W , но и W не больше W '. Чтобы доказать это, надо просто обратить предыдущие аргументы. Итак, если обе машины обратимы, то они должны производить одинаковую работу, и мы пришли к блестящему выводу Карно: если машина обратима, то безразлично, как она умудряется превращать тепло в работу. Произведенная машиной работа, если только машина поглощает определенное количество тепла при температуре Т 1и возвращает какую-то его часть при температуре Т 2, не зависит от устройства машины . Так уж устроен мир, и от частных свойств машины это не зависит.