Ричард Фейнман - Том 1. Механика, излучение и теплота

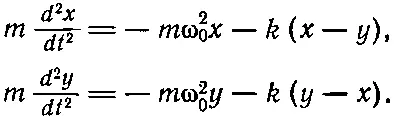(49.14)

Чтобы найти движение, при котором оба маятника колеблются с одинаковой частотой, мы должны определить, насколько отклоняется каждый из них. Другими словами, маятник А и маятник В будут колебаться с одинаковой частотой и с какими-то амплитудами А и B , отношение которых фиксировано. Давайте проверим, насколько подходит такое решение:

(49.15)

Если подставить его в уравнения (49.14) и собрать подобные члены, то получим

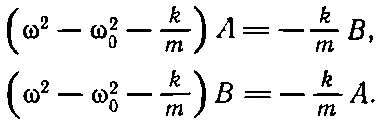(49.16)

При выводе этих уравнений мы сократили общий множитель е i ω t и разделили все на m.

Теперь мы видим, что получились два уравнения для, казалось бы, двух неизвестных. Однако на самом деле здесь не два неизвестных, ибо общие масштабы движения нельзя найти из этих уравнений. Они могут дать нам только отношение А к В, причем оба уравнения должны дать одинаковую величину . Требование согласованности уравнений друг с другом накладывает требование на частоту: она должна быть какой-то очень специальной.

Но найти частоту в этом частном случае довольно легко. Если перемножить оба уравнения, то мы получим

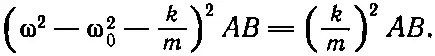(49.17)

В обеих сторонах можно сократить произведение АВ , за исключением тех случаев, когда либо А , либо В равно нулю, что означает отсутствие движения вообще. Но если движение есть, то должны быть равны между собой и другие сомножители, что приводит к квадратному уравнению. В результате получаются две возможные частоты:

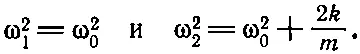(49.18)

Более того, если подставить эти значения частот снова в уравнения (49.16), то для первой частоты мы получим А = В , т. е. пружина вообще не будет растягиваться и оба маятника колеблются с частотой ω 0, как если бы пружины вообще не было. В другом решении, когда А =- В , пружина увеличивает восстанавливающую силу и частота возрастает. Более интересен случай, когда маятники имеют различные длины. Анализ этого случая, который очень похож на то, что мы недавно проделали, рекомендуем в качестве упражнения провести самим читателям.

Давайте теперь подытожим рассмотренные выше идеи, которые все являются аспектами, по-видимому, наиболее общего и удивительного принципа математической физики. Если у нас есть линейная система, характеристики которой не зависят от времени, то движение ее, вообще говоря, не обязано быть каким-то особенно простым. На самом деле оно может быть чрезвычайно сложным, однако существуют такие особые движения (обычно их целый ряд), при которых форма колебания синусоидально зависит от времени. Для колеблющихся систем, о которых сейчас шла речь, мы обычно получали мнимую экспоненту, но вместо того, чтобы сказать «экспоненциально», я предпочел сказать «синусоидально». Однако если стремиться к большей общности, то нужно говорить о каких-то особых движениях, очень специальной формы, изменяющихся экспоненциально со временем. Наиболее общее движение систем всегда можно представить в виде суперпозиции движений, включающих каждую из различных экспонент.

Есть смысл подчеркнуть еще раз специально для случая синусоидального движения: линейная система не обязательно должна двигаться чисто синусоидально, т. е. с одной определенной частотой, но как бы она ни двигалась, это движение можно представить в виде суперпозиции чисто синусоидальных колебаний. Частота каждого из этих колебаний, как и форма волны, зависит от свойств системы. Общее движение любой такой системы характеризуется заданием амплитуды и фазы каждой из гармоник при их сложении. Можно сказать это и по-другому: колебание любой линейной системы эквивалентно набору гармонических независимых осцилляторов, частоты которых соответствуют частотам собственных гармоник данной системы.

Эту главу мы закончим замечанием о связи гармоник с квантовой механикой. Колеблющимися объектами и величинами, которые изменяются со временем в квантовой механике, являются амплитуды вероятности, которые определяют вероятности обнаружения электрона или системы электронов в данном месте. Эта амплитуда может изменяться в пространстве и времени и удовлетворяет линейному уравнению. Но при переходе к квантовой механике происходит переименование. То, что мы называли частотой амплитуды вероятности, переходит в энергию в ее классическом смысле. Поэтому установленный выше принцип можно перевести на язык квантовой механики, заменив слово частота словом энергия . Получится примерно так: квантовомеханическая система, например атом, не обязательно обладает определенной энергией, точно так же, как простая механическая система не обязательно имеет определенную частоту, но каково бы ни было поведение системы, его всегда можно представить в виде суперпозиции состояний с определенной энергией. Энергия каждого состояния, как и форма амплитуды, которая дает вероятность нахождения частицы в различных местах, определяется свойствами атома. Общее движение может быть описано заданием амплитуд каждого из различных энергетических состояний. Именно здесь кроется причина возникновения энергетических уровней в квантовой механике. Поскольку квантовая механика все описывает в виде волн, то при некоторых обстоятельствах, когда электрон не обладает достаточной энергией, чтобы бесповоротно оторваться от протона, он представляет собой просто волну в ограниченном пространстве . Поэтому, так же как и для ограниченной струны, при решении волнового уравнения в квантовой механике в подобном случае возникают определенные дискретные частоты. В квантовомеханической интерпретации это будут определенные энергии . Следовательно, квантовомеханическая система, вследствие того что она описывается с помощью волн, может иметь определенные состояния с фиксированной энергией; примером могут служить дискретные энергетические уровни атомов.