Ричард Фейнман - Том 1. Механика, излучение и теплота

В качестве примера давайте найдем скорость падающего шара через 5 сек после начала падения. Один способ — это посмотреть по табл. 8.2, что происходило с шариком на пятой секунде. В течение этой секунды он прошел 45 м , так что, казалось бы, он падал со скоростью 45 м / сек . Однако это неверно, поскольку скорость его все время изменялась. Конечно, в среднем в течение этой секунды она составляла 45 м / сек , но в действительности шар ускорялся и в конце пятой секунды падал быстрее 45 м / сек . Наша задача состоит в том, чтобы определить скорость точно . Сделаем это следующим образом. Нам известно, где шарик находился через 5 сек . За 5 сек он прошел расстояние 125 м . К моменту 5,1 сек общее расстояние, которое прошел шарик, составит, согласно уравнению (8.1), 130,05 м . Таким образом, за дополнительную десятую долю секунды он проходит 5,05 м . А поскольку 5,05 м за 0,1 сек то же самое, что и 50,5 м / сек , то это и будет его скорость. Однако это все еще не совсем точно. Для нас совершенно неважно, будет ли это скорость в момент 5 сек , или в момент 5,1 сек , или где-то посредине. Наша задача вычислить скорость точно через 5 сек , а этого мы пока не сделали. Придется улучшить точность и взять теперь на тысячную долю больше 5 сек , т. е. момент 5,001 сек . Полное расстояние, пройденное за это время, составляет

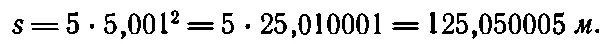
Следовательно, в последнюю тысячную долю секунды шарик проходит 0,050005 м , и если разделить это число на 0,001 сек , то получим скорость 50,005 м / сек . Это уже очень близко, но все же еще не точно . Однако теперь уже ясно, как поступить, чтобы найти скорость точно. Удобнее решать эту задачу в несколько более общем виде. Пусть требуется найти скорость в некоторый момент времени t 0(например, 5 сек ). Расстояние, которое пройдено к моменту t 0(назовем его s 0), будет 5 t 0 2(в нашем случае 125 м ). Чтобы определить расстояние, мы задавали вопрос: где окажется тело спустя время t 0+(небольшой добавок), или t 0+ε? Новое положение тела будет 5( t 0+ε) 2=5 t 2 0+10 t 0ε+5ε 2. (Это расстояние больше того расстояния, которое шарик прошел за t 0 сек, т. е . больше 5 t 0 2). Назовем это расстояние s 0+(небольшой добавок), или s 0+ x . Если теперь вычесть из него расстояние, пройденное к моменту t 0, то получим х — то дополнительное расстояние, которое шарик прошел за добавочное время ε, т. е. x=10t 0ε+5ε 2. Так что в первом приближении скорость будет равна

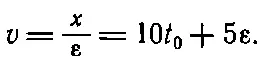(8.4)

Теперь мы уже знаем, что нужно делать, чтобы получить скорость точно в момент t 0: нужно брать отрезок ε все меньше и меньше, т. е. устремлять его к нулю. Таким путем из уравнения (8.4) получим

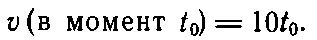
В нашей задаче t 0=5 сек , следовательно, скорость равна у=10·5=50 м / сек . Это и есть нужный ответ. Раньше, когда ε бралось равным 0,1 и 0,001 сек, получалась несколько большая величина, чем 50 м / сек , но теперь мы видим, что в действительности она в точности равна 50 м / сек .

Процедура, которую мы только что выполнили, настолько часто встречается в математике, что для величин ε и x было придумано специальное обозначение: ε обозначается как Δt, а х — как Δs. Величина Δt означает «небольшой добавок к t », причем подразумевается, что этот добавок можно делать меньше. Значок Δ ни в коем случае не означает умножение на какую-то величину, точно так же как sinθ не означает s·i·n·θ. Это просто некоторый добавок ко времени, причем значок Δ напоминает нам о его особом характере. Ну, а если Δ не множитель, то его нельзя сократить в отношении Δ s /Δ t . Это все равно, что в выражении sinθ/sin2θ сократить все буквы и получить 1/2. В этих новых обозначениях скорость равна пределу отношения Δ s /Δ t при Δ t , стремящемся к нулю, т. е.

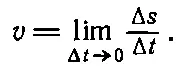(8.5)

Это по существу формула (8.3), но теперь яснее видно, что здесь все изменяется, а, кроме того, она напоминает, какие именно величины изменяются.

Существует еще один закон, который выполняется с хорошей точностью. Он гласит: изменение расстояния равно скорости, умноженной на интервал времени, за которое это изменение произошло, т. е. Δ s =vΔ t . Это правило строго справедливо только тогда, когда скорость не изменяется в течение интервала Δt, а это, вообще говоря, происходит, только когда Δ t достаточно мало. В таких случаях обычно пишут ds = vdt , где под dt подразумевают интервал времени Δ t при условии, что он сколь угодно мал. Если интервал Δt достаточно велик, то скорость за это время может измениться и выражение Δs=vΔt будет уже приближенным. Однако если мы пишем dt , то при этом подразумевается, что интервал времени неограниченно мал и в этом смысле выражение ds= vdt точное. В новых обозначениях выражение (8.5) имеет вид

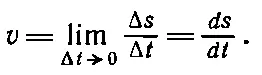
Величина ds / dt называется «производной s по t » (такое название напоминает о том, что изменяется), а сложный процесс нахождения производной называется, кроме того, дифференцированием. Если же ds и dt появляются отдельно, а не в виде отношения ds / dt , то они носят названия дифференциалов . Чтобы получше познакомить вас с новой терминологией, скажу еще, что в предыдущем параграфе мы нашли производную от функции 5 t 2, или просто производную от 5 t 2. Она оказалась равной 10 t . Когда вы больше привыкнете к новым словам, вам станет более понятна сама мысль. Для тренировки давайте найдем производную более сложной функции. Рассмотрим выражение s = At 3+ Bt + C , которое может описывать движение точки. Буквы A, B, C , так же как и в обычном квадратном уравнении, обозначают постоянные числа. Нам нужно найти скорость движения, описываемого этой формулой в любой момент времени t . Рассмотрим для этого момент t+Δt, причем к s прибавится некоторая добавка Δs, и найдем, как выражается Δs через Δt. Поскольку