Ричард Фейнман - Том 1. Механика, излучение и теплота

Чтобы ответить и на этот вопрос, положим, что у нас есть еще двое часов, целиком сходных между собой, скажем, с зубчатками и камнями, или основанных на радиоактивном распаде, или еще каких-нибудь. Опять согласуем их ход с нашими первыми часами. Пусть, пока свет прогуляется до конца и обратно, известив о своем прибытии тиканьем, за это время новая модель завершит свой цикл и тоже возвестит об этом какой-нибудь вспышкой, звонком или любым иным сигналом. Захватим с собой на космический корабль новую модель часов. Может быть, эти часы уже не отстанут, а будут идти так же, как их неподвижный двойник. Ах, нет! Если они разойдутся с первой моделью (которая тоже находится на корабле), то человек сможет использовать этот разнобой между показаниями обоих часов, чтобы определить скорость корабля. А ведь считается, что скорость узнать немыслимо. Смотрите, как ловко! Нам не нужно ничего знать о механизме работы новых часов, не нужно знать, что именно в них замедляется, мы просто знаем, что, какова бы ни была причина, ход часов будет выглядеть замедленным, и притом в любых часах одинаково.

Что же выходит? Если все движущиеся часы замедляют свой ход, если любой способ измерения времени приводит к замедленному темпу течения времени, нам остается только сказать, что само время , в определенном смысле, кажется на движущемся корабле замедленным. На корабле все: и пульс космонавта, и быстрота его соображения, и время, потребное для зажигания папиросы, и период возмужания и постарения — все это должно замедлиться в одинаковой степени, ибо иначе можно будет узнать, что корабль движется. Биологи и медики иногда говорят, что у них нет уверенности в том, что раковая опухоль будет в космическом корабле развиваться дольше. Однако с точки зрения современного физика это случится почти наверняка; в противном случае можно было бы по быстроте развития опухоли судить о скорости корабля!

Очень интересным примером замедления времени при движении снабжают нас мю-мезоны (мюоны) — частицы, которые в среднем через 2,2·10 -6 сек самопроизвольно распадаются. Они приходят на Землю с космическими лучами, но могут быть созданы и искусственно в лаборатории. Часть космических мюонов распадается еще на большой высоте, а остальные — только после того, как остановятся в веществе. Ясно, что при таком кратком времени жизни мюон не может пройти больше 600 м , даже если он будет двигаться со скоростью света. Но хотя мюоны возникают на верхних границах атмосферы, примерно на высоте 10 км и выше, их все-таки обнаруживают в земных лабораториях среди космических лучей. Как это может быть? Ответ состоит в том, что разные мюоны летят с различными скоростями, иногда довольно близкими к скорости света. С их собственной точки зрения они живут всего лишь около 2 мксек , с нашей же — их жизненный путь несравненно более долог, достаточно долог, чтобы достигнуть поверхности Земли. Их жизнь удлиняется в 1/√(1- u 2/ c 2) раз. Среднее время жизни мюонов разных скоростей было точно измерено, причем полученное значение хорошо согласуется с формулой.

Мы не знаем, почему мезон распадается и каков его внутренний механизм, но зато мы знаем, что его поведение удовлетворяет принципу относительности. Тем и полезен этот принцип — он позволяет делать предсказания даже о тех вещах, о которых другим путем мы мало чего узнаем. К примеру, еще не имея никакого представления о причинах распада мезона, мы все же можем предсказать, что если его скорость составит 9/ 10скорости света, то кажущаяся продолжительность отведенного ему срока жизни будет равна 2,2·10 -6/√(1-9 2/10 2) сек . И это предсказание оправдывается. Правда, неплохо?

Теперь мы вернемся к преобразованию Лоренца (15.3) и попытаемся лучше понять связь между системами координат ( x, y , z, t ) и ( х ', у ', z ', t '). Будем называть их системами S и S ', или соответственно системами Джо и Мика. Мы уже отметили, что первое уравнение основывается на предположении Лоренца о том, что по направлению х все тела сжимаются. Как же можно доказать, что такое сокращение действительно бывает? Мы уже понимаем, что в опыте Майкельсона — Морли по принципу относительности поперечное плечо ВС не может сократиться; в то же время нулевой результат опыта требует, чтобы времена были равны. Чтобы получился такой результат, приходится допустить, что продольное плечо BE кажется сжатым в отношении √(1- u 2/ с 2). Что означает это сокращение на языке Джо и Мика? Положим, что Мик, двигаясь с системой S ' в направлении х ', измеряет метровой линейкой координату х ' в некоторой точке. Он прикладывает линейку х ' раз и думает, что расстояние равно х ' метрам. С точки же зрения Джо, (в системе S ) линейка у Мика в руках укорочена, а «на самом деле» отмеренное им расстояние равно x'√(1- u 2/ с 2) метров. Поэтому если система S ' удалилась от системы S на расстояние ut , то наблюдатель в системе S должен сказать, что эта точка (в его координатах) удалена от начала на x = x '√(1- u 2/ c 2)+ ut , или

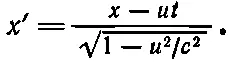
Это и есть первое уравнение из преобразований Лоренца.

Подобным же образом из-за различия в масштабах времени появляется и знаменатель в уравнении (15.Зг) в преобразованиях Лоренца. Самое интересное в этом уравнении — это новый и неожиданный член в числителе, член ux / с 2. В чем его смысл? Внимательно вдумавшись в положение вещей, можно понять, что события, происходящие, по мнению Мика (наблюдателя в системе S'), в разных местах одновременно, с точки зрения Джо (в системе S ), вовсе не одновременны. Когда одно событие случилось в точке x 1в момент t 0, а другое — в точке х 2в тот же момент t 0, то соответствующие моменты t ' 1и t ' 2отличаются на

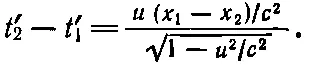
Это явление можно назвать «нарушением одновременности удаленных событий». Чтобы пояснить его, рассмотрим следующий опыт.

Пусть человек, движущийся в космическом корабле (система S '), установил в двух концах корабля часы. Он хочет знать, одинаково ли они идут. Как синхронизовать ход часов? Это можно сделать по-разному. Вот один из способов, он почти не требует вычислений. Расположимся как раз где-то посредине между часами. Из этой точки пошлем в обе стороны световые сигналы. Они будут двигаться в обоих направлениях с одинаковой скоростью и достигнут обоих часов в одно и то же время. Вот этот-то одновременный приход сигналов и можно применить для согласования хода. Положим, что человек в S ' таким способом согласует ход часов. Посмотрим, согласится ли наблюдатель в системе S , что эти часы идут одинаково. Космонавт в системе S ' имеет право верить, что их ход одинаков; ведь он не знает, что он движется. Но наблюдатель в системе S сразу рассудит, что раз корабль движется, то часы на носу корабля удалились от светового сигнала и свету пришлось пройти больше половины длины корабля, прежде чем он достиг часов; часы на корме, наоборот, двигались к световому сигналу — значит, его путь сократился. Поэтому сигнал сперва дошел до часов на корме, хотя космонавту в системе S ' показалось, что сигналы достигли обоих часов одновременно. Итак, выходит, что когда космонавт считает, что события в двух местах корабля произошли одновременно (при одном и том же значении t' в его системе координат), то в другой системе координат одинаковым t ' отвечают разные значения t !