Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
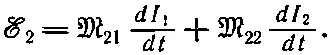 (17.31)
(17.31)
Аналогично, э. д. с. в катушке 1 будет зависеть не только от изменяющегося тока в катушке 2, но и от изменяющегося тока в ней самой:
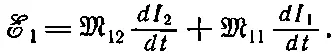 (17.32)
(17.32)
Коэффициенты M 22и M 11всегда отрицательны. Обычно пишут
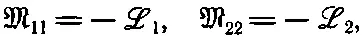 (17.33)
(17.33)
где ℒ 1и ℒ 2называют коэффициентами самоиндукции двух катушек (или индуктивностями).
Конечно, э. д. с. самоиндукции будет существовать даже для одной катушки. Любая катушка сама по себе обладает коэффициентом самоиндукции ℒ, и ее э. д. с. будет пропорциональна скорости изменения тока в катушке. Обычно считают, что э. д. с. и ток одной катушки положительны, если они направлены одинаково. При этом условии для отдельной катушки можно написать
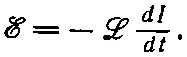 (17.34)
(17.34)
Знак минус указывает на то, что э. д. с. противодействует изменению тока, ее часто называют «обратной э. д. с.».
Поскольку любая катушка обладает самоиндукцией, противодействующей изменению тока, ток в катушке обладает своего рода инерцией. Действительно, если мы хотим изменить ток в катушке, мы должны преодолеть эту инерцию, присоединяя катушку к какому-то внешнему источнику, например батарее или генератору (фиг. 17.10, а ).
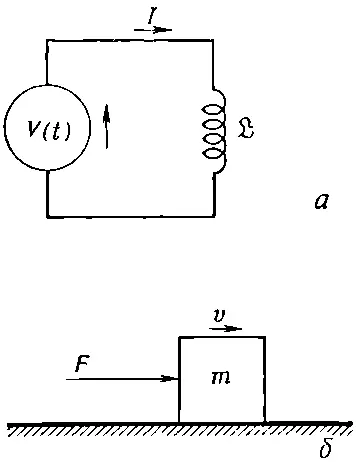
Фиг. 17.10. Цепь с источником напряжения и индуктивностью (а) и аналогичная ей механическая система (б).
В такой цепи ток I связан с напряжением V соотношением
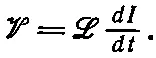 (17.35)
(17.35)
Это соотношение имеет форму уравнения движения Ньютона для частицы в одном измерении. Поэтому мы можем исследовать его по принципу «одинаковые уравнения имеют одинаковые решения». Таким образом, если поставить в соответствие напряжение V от внешнего источника приложенной внешней силе F , а ток I в катушке скорости v частицы, то коэффициент индукции катушки ℒ будет соответствовать массе m частицы [21] Кстати, это не единственный способ установления соответствия между механическими и электрическими величинами.
(фиг. 17.10, б ).
Таблица 17.1. СОПОСТАВЛЕННЫЕ ВЕЛИЧИНЫ
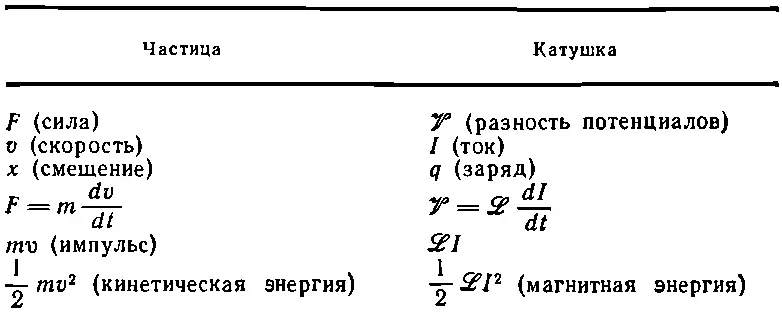
§ 8. Индуктивность и магнитная энергия
Продолжая аналогию предыдущего параграфа, мы отметили в таблице, что в соответствии с механическим импульсом p = mv (скорость изменения которого равна приложенной силе) должна существовать аналогичная величина, равная ℒI , скорость изменения которой V . Разумеется, мы не имеем права говорить, что ℒ I — это настоящий импульс цепи; на самом деле это вовсе не так. Вся цепь может быть неподвижна и вообще не иметь импульса. Просто ℒ I аналогично импульсу mv в смысле удовлетворения аналогичным уравнениям. Точно так же кинетической энергии 1/ 2mv 2здесь соответствует аналогичная величина 1/ 2ℒI 2. Но здесь нас ждет сюрприз. Величина 1/ 2 ℒI 2— действительно есть энергия и в электрическом случае. Так получается потому, что работа, совершаемая в единицу времени над индуктивностью, равна VI , а в механической системе она равна Fv — соответствующей величине. Поэтому в случае энергии величины не только соответствуют друг другу в математическом смысле, но имеют еще и одинаковое физическое значение.
Мы можем проследить это более подробно. В (17.16) мы нашли, что электрическая работа в единицу времени за счет сил индукции есть произведение э. д. с. и тока:
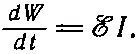
Подставляя вместо ℰ ее выражение через токи из (17.34), имеем
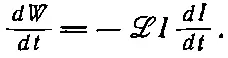 (17.36)
(17.36)
Интегрируя это уравнение, находим, что энергия, которая требуется от внешнего источника, чтобы преодолеть э. д. с. самоиндукции и создать ток [22] Мы пренебрегаем всеми тепловыми потерями энергии в сопротивлении катушки. Эти потери требуют дополнительных затрат энергии источника, но не меняют энергии, которая тратится на индуктивность.
(что должно равняться накопленной энергии U), равна
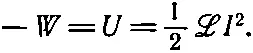 (17.37)
(17.37)
Поэтому энергия, накопленная в индуктивности, равна 1/ 2ℒ I 2.Применяя те же рассуждения к паре катушек, изображенных на фиг. 17.8 или 17.9, мы можем показать, что полная электрическая энергия системы дается выражением
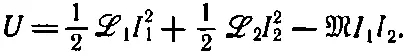 (17.38)
(17.38)
В самом деле, начиная с тока I=0 в обеих катушках, можно вначале включить ток I 1в катушке 1, оставляя I 2=0. Совершенная работа как раз равна 1/ 2ℒ 1 I 1 2. Но теперь, включая I 2, мы совершаем не только работу 1/ 2ℒ 2I 2 2против э. д. с. в цепи 2, но еще и добавочное количество работы —MI 1I 2, которая есть интеграл от э. д. с. M( dI 2/ dt ) в цепи 1, умноженный на теперь уже постоянный ток I 1в этой цепи.
Пусть теперь нам нужно найти силу между любыми двумя катушками, по которым идут токи I 1и I 2. Прежде всего мы могли бы использовать принцип виртуальной работы, взяв вариацию от энергии (17.38). Мы должны помнить, конечно, что при изменении относительного положения катушек единственной меняющейся величиной является коэффициент взаимной индукции M. Тогда мы могли бы записать уравнение виртуальной работы в виде
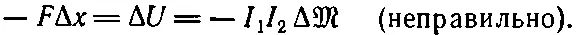
Это уравнение ошибочно, потому что, как мы видели раньше, в него включено только изменение энергии двух катушек и не включена энергия источников, которые поддерживают постоянными значения токов I 1и I 2. Мы понимаем теперь, что эти источники должны поставлять энергию для компенсации индуцированных э. д. с. в катушках во время их движения. Если мы хотим правильно применить принцип виртуальной работы, то должны включить и эти энергии. Но мы видели, что можно сделать и короче — использовать принцип виртуальной работы, помня, что полная энергия — это взятая с обратным знаком энергия U мех(то что мы называем «механической энергией»). Поэтому силу можно записать в виде
Читать дальшеИнтервал:
Закладка:






