Ричард Фейнман - Том 2. Электромагнетизм и материя

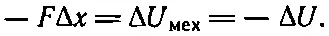(17.39)

Тогда сила между катушками дается выражением

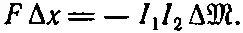
Воспользуемся выражением (17.38) для энергии системы из двух катушек, чтобы показать, какое интересное неравенство существует между взаимной индукцией M и коэффициентами самоиндукции ℒ 1и ℒ 2двух катушек. Ясно, что энергия двух катушек должна быть положительной. Если мы начинаем с нулевых токов в обеих катушках и увеличиваем эти токи до некоторых значений, то тем самым мы увеличиваем энергию всей системы. В противном случае токи самопроизвольно возрастут и будут отдавать энергию остальному миру — вещь невероятная! Далее, наше выражение для энергии (17.38) можно с таким же успехом записать в следующей форме:

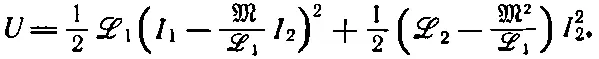(17.40)

Это просто алгебраическое преобразование. Эта величина должна быть всегда положительна при любых значениях I 1и I 2. В частности, она должна быть положительна, когда I 2вдруг примет особое значение:

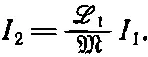(17.41)

Но при таком значении I 2первое слагаемое в (17.40) равно нулю. Если энергия положительна, то последнее слагаемое в (17.40) должно быть больше нуля. Мы получаем требование, что

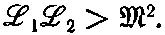
Таким образом, мы доказали общее соотношение, что величина взаимной индукции M любых двух катушек обязательно меньше или равна геометрическому среднему двух коэффициентов самоиндукции (сам M может быть положителен или отрицателен в зависимости от выбора знаков для токов I 1и I 2):

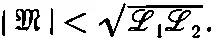(17.42)

Соотношение между M и коэффициентами самоиндукции обычно записывают в виде

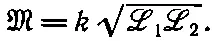(17.43)

Постоянную k называют коэффициентом связи . Если большая часть потока от одной катушки проходит через другую катушку, то коэффициент связи близок к единице; мы говорим, что катушки «сильно связаны». Если катушки значительно удалены друг от друга или же все устроено так, что взаимное проникновение их потоков очень мало, коэффициент связи становится близок к нулю, а коэффициент взаимной индукции очень мал.

Для вычисления взаимной индукции двух катушек мы дали формулу (17.30), которая представляет собой двойной контурный интеграл по обеим цепям. Мы могли бы подумать, что та же формула применима и для вывода коэффициента самоиндукции одной катушки, если оба контурных интегрирования проводить по одной и той же катушке. Однако это не так, потому что при интегрировании по двум катушкам знаменатель r 12под знаком интеграла стремится к нулю, когда два элемента длины находятся в одной точке. Коэффициент самоиндукции, получаемый из этой формулы, оказывается бесконечным. Происходит это потому, что формула наша — приближенная, и справедлива она только для поперечных сечений проводов в обеих цепях, малых по сравнению с расстоянием от одной цепи до другой. Ясно, что это приближение для отдельной катушки не годится. На самом деле оказывается, что индуктивность отдельной катушки стремится логарифмически к бесконечности, когда диаметр ее проволоки становится все меньше и меньше.

Значит, мы должны поискать другой способ вычисления коэффициента самоиндукции одной катушки. При этом надо учесть распределение токов внутри проводника, потому что его размеры — важный параметр. Но мы не будем считать полную индуктивность, а сосчитаем лишь ту ее часть, которая связана с расположением проводников, и не будем учитывать часть, связанную с распределением токов. Пожалуй, самый простой способ найти такую индуктивность — это использовать магнитную энергию. Ранее, в гл. 15, § 3, мы нашли выражение для магнитной энергии распределения стационарных токов:

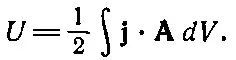(17.44)

Если известно распределение плотности тока j, то можно вычислить векторный потенциал А, а затем, оценив интеграл (17.44), получить энергию. Эта энергия равна магнитной энергии самоиндукции, 1/ 2ℒ I 2. Приравнивая их, получаем формулу для индуктивности:

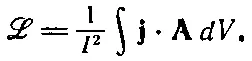(17.45)

Мы, конечно, ожидаем, что индуктивность есть число, зависящее только от геометрии цепи, а не от тока I в цепи. Формула (17.45) действительно приводит к такому результату, потому что интеграл в ней пропорционален квадрату тока — ток входит один раз от jи еще раз от векторного потенциала А. Интеграл, деленный на I 2, зависит от геометрии цепи, но не от тока I.

Выражению (17.44) для энергии распределения токов можно придать совсем другую форму, иногда более удобную для вычислений. Кроме того, как мы увидим позже, именно эта форма важна, потому что она справедлива в более общем случае. В формуле (17.44) и Аи jможно связать с В, поэтому можно надеяться, что энергия выразится через магнитное поле — точно так же, как нам удалось связать электростатическую энергию с электрическим полем. Начнем с подстановки ε 0c 2 ∇× Bвместо j. Заменить Амы не можем с той же легкостью, потому что нельзя обратить B= ∇× A, чтобы выразить Ачерез В. Можно только записать

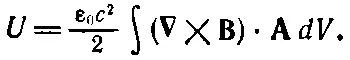(17.46)

Любопытно, что при некоторых ограничениях этот интеграл можно превратить в

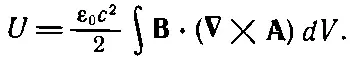(17.47)

Чтобы увидеть это, выпишем подробно типичный множитель. Предположим, что мы взяли множитель ( ∇× B) z A z, входящий в интеграл (17.46). Выписывая полностью компоненты, получаем

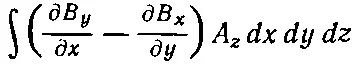
(имеются, конечно, еще два интеграла того же сорта). Проинтегрируем теперь первый множитель по х , интегрируя по частям, т. е.