Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
На фиг. 17.8 показано устройство из двух катушек, с помощью которого можно продемонстрировать основные эффекты, ответственные за работу трансформатора.
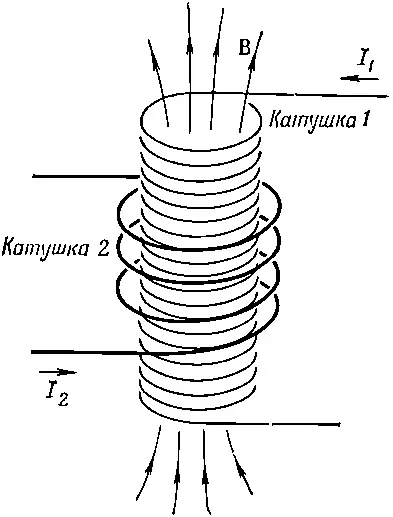
Фиг. 17.8. Ток в катушке 1 создает магнитное поле, проходящее через катушку 2.
Катушка 1 состоит из проводящей проволоки, свитой в виде длинного соленоида. Вокруг этой катушки и изолированно от нее навита катушка 2, состоящая из нескольких витков проволоки. Если теперь по катушке 1 пропустить ток, то, как мы знаем, внутри нее появится магнитное поле. Это магнитное поле проходит также сквозь катушку 2. Когда ток в катушке 1 меняется, магнитный поток тоже будет меняться, и в катушке 2 появится индуцированная э.д.с. Эту индуцированную э.д.с. мы сейчас и вычислим.
В гл. 13, § 5 (вып. 5) мы видели, что магнитное поле внутри длинного соленоида однородно и равно
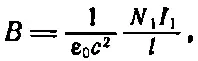 (17.23)
(17.23)
где N 1— число витков в катушке 1, I 1— ток в ней, а l — её длина. Пусть поперечное сечение катушки 1 равно S, тогда поток поля Вравен его величине, умноженной на S. Если в катушке 2 имеется N 2витков, то поток проходит по катушке N 2раз. Поэтому э. д. с. в катушке 2 дается выражением
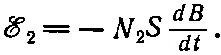 (17.24)
(17.24)
Единственная меняющаяся со временем величина в (17.23) есть I 1. Поэтому э. д. с. дается выражением
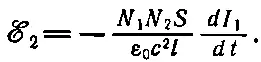 (17.25)
(17.25)
Мы видим, что э. д. с. в катушке 2 пропорциональна скорости изменения тока в катушке 1. Константа пропорциональности — по существу геометрический фактор двух катушек, называется коэффициентом взаимной индукции и обозначается обычно M 21. Тогда (17.25) записывается уже в виде
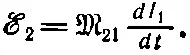 (17.26)
(17.26)
Предположим теперь, что нам нужно было бы пропустить ток через катушку 2 и нас интересует, чему равна э. д. с. в катушке 1. Мы вычислили бы магнитное поле, которое повсюду пропорционально току I 2. Поток сквозь катушку I зависел бы от геометрии, но был бы пропорционален току I 2. Поэтому э. д. с. в катушке 1 снова была бы пропорциональна dI 2/ dt . Мы можем записать
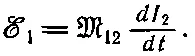 (17.27)
(17.27)
Вычисление M 12было бы труднее, чем те вычисления, которые мы проделали для M 21. Мы не будем сейчас им заниматься, потому что дальше в этой главе мы покажем, что M 12обязательно равно M 21.
Поскольку поле любой катушки пропорционально текущему в ней току, такой же результат получился бы и для любых двух катушек из проволоки. Выражения (17.26) и (17.27) приобрели бы одинаковую форму, и только постоянные M 12и M 21были бы другие. Их значения будут зависеть от формы катушек и их относительного положения.
Предположим, нам нужно найти коэффициент взаимной индукции между двумя произвольными катушками, например показанными на фиг. 17.9.
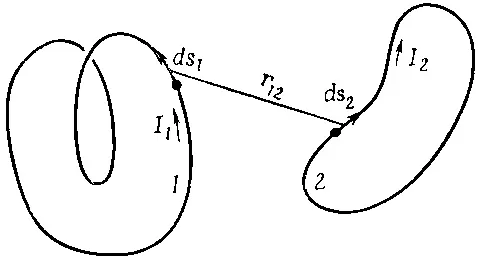
Фиг. 17.9. Любые две катушки обладают взаимной индукцией m, пропорциональной интегралу от ds 1 ·ds 2 ·(1/r 12 ).
Мы знаем, что общее выражение для э. д. с. в катушке 1 можно записать так:
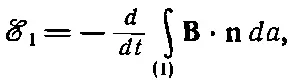
где В— магнитное поле, а интеграл берется по поверхности, ограниченной контуром 1. В гл. 14, § 1 (вып. 5) мы видели, что поверхностный интеграл от Вможно свести к контурному интегралу от векторного потенциала. В нашем случае
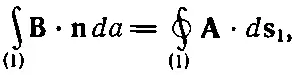
где А— векторный потенциал, а ds 1— элемент цепи 1. Контурный интеграл берется вдоль контура 1, поэтому э.д.с. в этой катушке может быть записана в виде
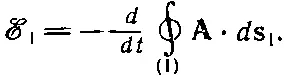
Теперь предположим, что векторный потенциал цепи 1 возникает за счет токов в цепи 2. Тогда его можно записать как контурный интеграл по контуру цепи 2:
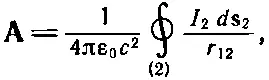 (17.29)
(17.29)
где I 2— ток в цепи 2, а r 12— расстояние от элемента цепи ds 2 к точке на контуре 1, в которой мы вычисляем векторный потенциал (см. фиг. 17.9). Комбинируя (17.28) и (17.29), можно выразить э. д. с. в цепи 1 как двойной контурный интеграл:
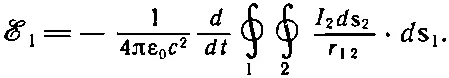
В этом выражении все интегралы берутся по неподвижным контурам. Единственной переменной величиной является ток I 2, который не зависит от переменных интегрирования. Поэтому его можно вынести за знак интеграла. Тогда э. д. с. можно записать как
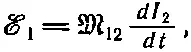
где коэффициент M 12равен
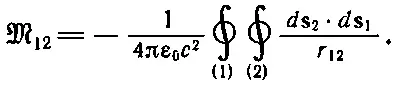 (17.30)
(17.30)
Из этого интеграла очевидно, что M 12зависит только от геометрии цепей; он зависит от некоторого среднего расстояния между двумя цепями, причем в среднее с наибольшим весом входят параллельные отрезки проводников двух катушек. Нашу формулу можно использовать для вычисления коэффициента взаимной индукции любых двух цепей произвольной формы. Кроме того, она показывает, что интеграл для M 12тождествен с интегралом для M 21. Таким образом, мы показали, что оба коэффициента одинаковы. Для системы только с двумя катушками коэффициенты M 12и M 21часто обозначают символом M без значков и называют просто коэффициентом взаимной индукции :
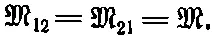
§ 7. Самоиндукция
При обсуждении индуцированных э. д. с. в двух катушках на фиг. 17.8 и 17.9 мы рассмотрели лишь случай, когда ток проходит либо в одной катушке, либо в другой. Если токи имеются одновременно в обеих катушках, то магнитный поток, пронизывающий каждую катушку, будет представлять сумму двух потоков, существующих и по отдельности, поскольку к магнитным полям применим принцип суперпозиции. Поэтому э. д. с. в каждой катушке будет пропорциональна не только изменению тока в другой катушке, но и изменению тока в ней самой. Таким образом, полную э. д. с. в катушке 2 следует записать в виде [20] Знак M 12 и M 21 в (17.31) и (17.32) зависит от произвола в выборе положительного направления токов в обеих катушках.
Интервал:
Закладка:






