Ричард Фейнман - Том 2. Электромагнетизм и материя

Рассматривая уравнения Максвелла порознь, нелегко сразу получить решение. Поэтому сначала мы сообщим вам ответ, а затем уже проверим, действительно ли оно удовлетворяет уравнениям. Ответ : Поле В, которое мы вычислили, на самом деле создается прямо вблизи листа с током (для малых х ). Так и должно быть, потому что если мы проведем крошечную петлю вокруг листа, то в ней не будет места для прохождения электрического потока. Но поле Вподальше (для больших х ) сначала равно нулю. Оно в течение некоторого времени остается нулевым, а затем внезапно включается. Короче говоря, мы включаем ток и немедленно вблизи него включается магнитное поле с постоянным значением В; затем включенное поле Враспространяется от области источника. Через некоторое время появляется однородное магнитное поле всюду, вплоть до некоторого значения х , а за ним оно равно нулю. Вследствие симметрии оно распространяется как в положительном, так и в отрицательном x-направлении.

Поле Еделает то же самое. До момента t=0 (когда мы включаем ток) поле повсюду равно нулю. Затем, спустя время t , как Е, так и Впостоянны вплоть до расстояния х = vt, а за ним равны нулю. Поля продвигаются вперед, подобно приливной волне, причем фронт их движется с постоянной скоростью, которая оказывается равной с , но пока мы будем называть ее v . Изображение зависимости величины Еили Вот х (как они кажутся в момент t ) показано на фиг. 18.4, а .

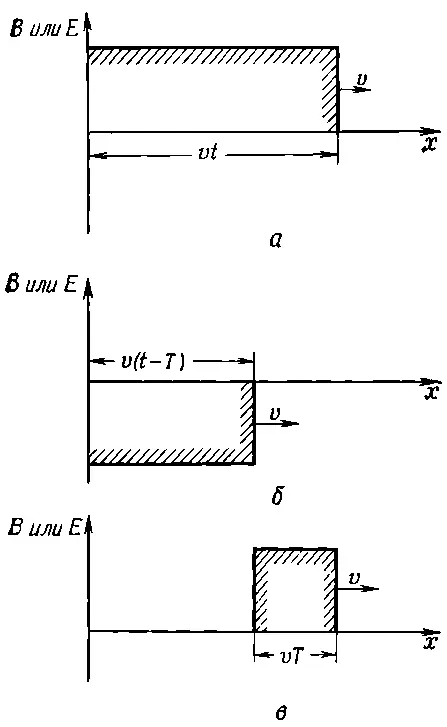
Фиг. 18.4. Зависимость величины В (или E) от х. а — спустя время t после начала движения заряженной плоскости; б — поля от заряженной плоскости, начавшей двигаться в момент t=T в сторону отрицательных у; в — сумма а и б.

Если снова посмотреть на фиг. 18.3 в момент t , то мы увидим, что область между x =± vt «занята» полями, но они еще не достигли области за ней. Мы снова подчеркиваем — мы предполагаем, что лист заряжен, а следовательно, поля Еи Впростираются бесконечно далеко в у - и z-направлениях. (Мы не можем изобразить бесконечный лист, поэтому мы показываем лишь то, что происходит в конечной области.)

Теперь мы хотим проанализировать количественно то, что происходит. Чтобы сделать это, рассмотрим два поперечных разреза: вид сверху, если смотреть вниз вдоль оси у (фиг. 18.5), и вид сбоку, если смотреть назад вдоль оси z (фиг. 18.6).

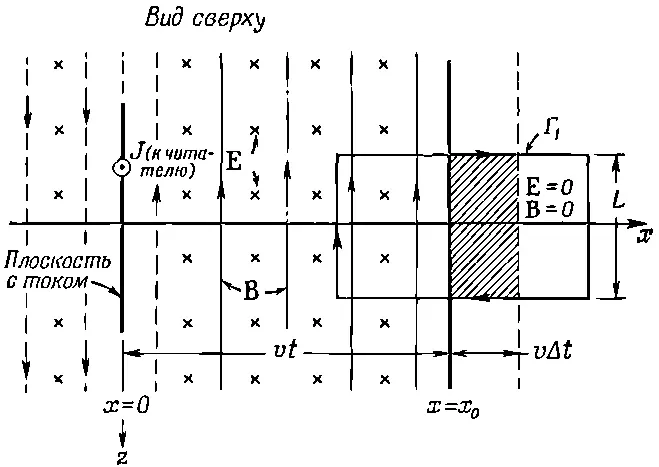
Фиг. 18.5. То же, что на фиг. 18.3 (вид сверху).

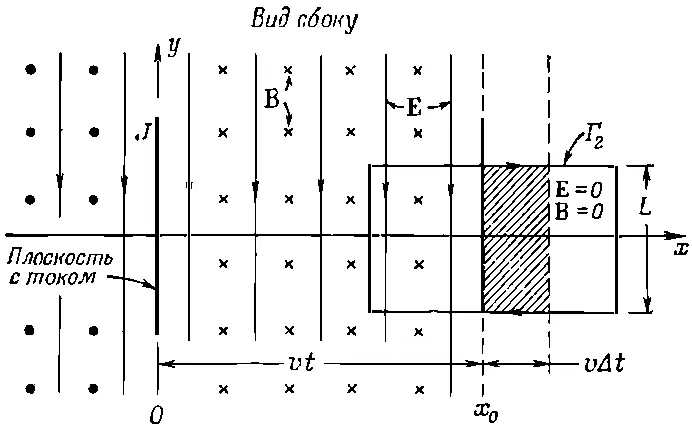
Фиг. 18.6. То же, что на фиг. 18.3 (вид сбоку).

Начнем с вида сбоку. Мы видим заряженный лист, движущийся вверх; магнитное поле направлено внутрь страницы для +x и от страницы для - х , а электрическое поле направлено вниз всюду, вплоть до x =± vt .

Посмотрим, согласуются ли такие поля с уравнениями Максвелла. Сначала нарисуем одну из тех петель, которыми мы пользовались для вычисления контурного интеграла, скажем прямоугольник Г 2на фиг. 18.6. Заметьте, что одна сторона прямоугольника проходит в области, где есть поля, а другая — в области, до которой поля еще не дошли. Через эту петлю проходит какой-то магнитный поток. Если он изменяется, должна появиться э. д. с. вдоль петли. Если волновой фронт движется, мы будем иметь меняющийся магнитный поток, поскольку поверхность, внутри которой существует поле В, непрерывно увеличивается со скоростью v . Поток внутри Г 2равен произведению Вна ту часть поверхности внутри Г 2, где есть магнитное поле. Скорость изменения потока (поскольку величина Впостоянна) равна величине поля, умноженной на скорость изменения поверхности. Скорость изменения поверхности найти легко. Если ширина прямоугольника Г 2равна L , то поверхность, в которой Всуществует, меняется как Lv Δ t за отрезок времени Δt (см. фиг. 18.6). Скорость изменения потока тогда равна BLv . По закону Фарадея она должна быть равна контурному интегралу от Евокруг Г 2, который есть просто EL . Мы получаем равенство

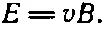(18.10)

Таким образом, если отношение Е к В равно v , то рассматриваемые нами поля будут удовлетворять уравнению Фарадея.

Но это не единственное уравнение; у нас есть еще одно, связывающее Еи В:

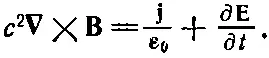(18.11)

Чтобы применить это уравнение, посмотрим на вид сверху, изображенный на фиг. 18.5. Мы уже видели, что это уравнение дает нам значение В вблизи заряженного листа. Кроме того, для любой петли, нарисованной вне листа, но позади волнового фронта, нет ни ротора В, ни jили меняющегося поля Е, так что уравнение там справедливо. А теперь посмотрим, что происходит в петле Г 1, которая пересекает волновой фронт, как показано на фиг. 18.5. Здесь нет токов, поэтому уравнение (18.11) можно записать в интегральной форме так:

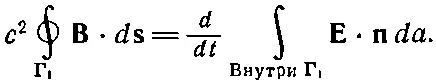(18.12)

Контурный интеграл от Весть просто произведение В на L . Скорость изменения потока Евозникает только благодаря продвигающемуся волновому фронту. Область внутри Г 1, где Ене равно нулю, увеличивается со скоростью vL . Правая сторона (18.12) тогда равна vLE . Уравнение это приобретает вид

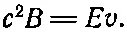(18.13)

Мы имеем решение, когда поля Ви Епостоянны за фронтом, причем оба направлены под прямыми углами к направлению, в котором движется фронт, и под прямыми углами друг к другу. Уравнения Максвелла определяют отношение Е к В . Из (18.10) и (18.13) получаем

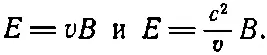
Но одну минутку! Мы нашли два разных выражения для отношения Е / В . Может ли такое поле, как мы описываем, действительно существовать? Имеется лишь одна скорость v, для которой оба уравнения могут быть справедливы, а именно v = с . Волновой фронт должен передвигаться со скоростью с. Вот пример, когда электрическое возмущение от тока распространяется с определенной конечной скоростью с .