Ричард Фейнман - Том 2. Электромагнетизм и материя

Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.

Начнем с ∇· В=0 — простейшего из уравнений. Мы знаем, что оно подразумевает, что В— есть ротор чего-то. Поэтому, если вы записали

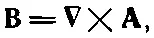(18.16)

то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А', если A'= A+ ∇ψ, где ψ— любое скалярное поле, потому что ротор ∇ψ — нуль и В— по-прежнему то же самое. Мы говорили об этом раньше.)

Теперь разберем закон Фарадея ∇× E=-∂ B/∂ t , потому что он не содержит никаких токов или зарядов. Если мы запишем Вкак ∇× Aи продифференцируем по t , то сможем переписать закон Фарадея в форме

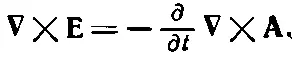
Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде

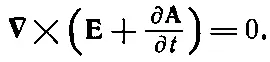(18.17)

Мы видим, что Е+∂ A/∂ t — это вектор, ротор которого равен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было ∇× E=0, и мы тогда решили, что Е— само градиент чего-то. Пусть это градиент от -φ (минус для технических удобств). То же самое сделаем и для E+∂ A/∂ t ; мы полагаем

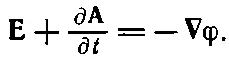(18.18)

Мы используем то же обозначение φ, так что в электростатическом случае, когда ничто не меняется со временем и ∂ A/∂ t исчезает, Ебудет нашим старым - ∇φ. Итак, закон Фарадея можно представить в форме

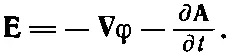(18.19)

Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Еи Внужны четыре потенциальные функции: скалярный потенциал φ и векторный потенциал А, который, разумеется, представляет три функции.

Итак, А определяет часть Е, так же как и В. Что же произойдет, когда мы заменим Ана A'= A+ ∇ψ? В общем, Едолжно было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что Аизменяется так, чтобы не влиять на поля Еи В(т. е. не меняя физики), если будем всегда изменять Аи φ вместе по правилам

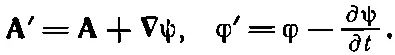(18.20)

Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.

Раньше мы выбирали ∇· А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.

Сейчас мы вернемся к двум оставшимся уравнениям Максвелла, которые свяжут потенциалы и источники ρ и j. Раз мы можем определить Аи φ из токов и зарядов, то можно всегда получить Еи Виз уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.

Начнем с подстановки уравнения (18.19) в ∇· E=ρ/ε 0; получаем

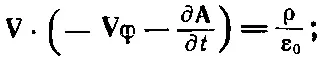
это можно записать еще в виде

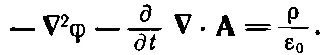(18.21)

Таково первое уравнение, связывающее φ и Ас источниками.

Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:

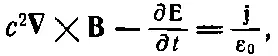
а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):

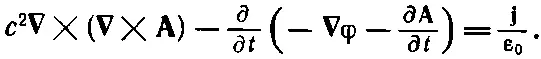
Первый член можно переписать, используя алгебраическое тождество ∇×( ∇× A)= ∇( ∇· A)- ∇ 2 A; мы получаем

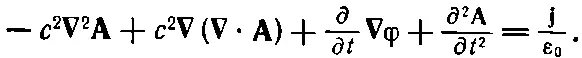(18.22)

Не очень-то оно простое!

К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для Аи для φ разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая [25] Выбор значения ∇·А называется «выбором калибровки». Изменение А за счет добавления ∇ψ называется «калибровочным преобразованием». Выбор (18.23) называют «калибровкой Лоренца».

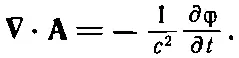(18.23)

Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:

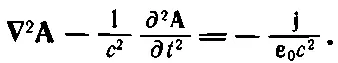(18.24)

И. наше уравнение (18.21) для φ принимает такую же форму:

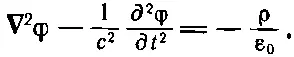(18.25)

Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит φ, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (∂/∂ t ) 2, когда мы раскроем ее, то обнаружим

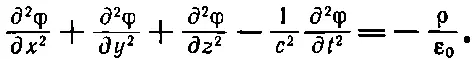(18.26)

Это уравнение имеет приятную симметрию по х, у, z, t ; здесь (-1/ с 2) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.