Ричард Фейнман - Том 2. Электромагнетизм и материя

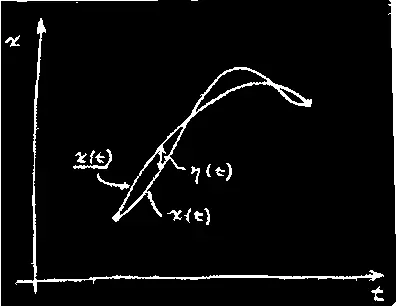
Идея состоит в том, что если мы подсчитаем действие S на пути x ( t ), то разность между этим S и тем действием, которое мы вычислили для пути x ( t ) (для простоты оно будет обозначено _S), или разность между _S и S, должна быть в первом приближении по η нулем. Они могут отличаться во втором порядке, но в первом разность обязана быть нулем.

И это должно соблюдаться для любой η. Впрочем, не совсем для любой. Метод требует принимать во внимание только те пути, которые все начинаются и кончаются в одной и той же паре точек, т. е. всякий путь должен начинаться в определенной точке в момент t 1и кончаться в другой определенной точке в момент t 2. Эти точки и моменты фиксируются. Так что наша функция η (отклонение) должна быть равна нулю на обоих концах: η(t 1)=0 и η(t 2)=0. При этом условии наша математическая задача становится полностью определенной.

Если бы вы не знали дифференциального исчисления, вы могли бы проделать такую же вещь для отыскания минимума обычной функции f ( x ). Вы бы задумались над тем, что случится, если взять f ( x ) и прибавить к х малую величину h , и доказывали бы, что поправка к f ( x ) в первом порядке по h должна в минимуме быть равна нулю. Вы бы подставили x + h вместо х и разложили бы f ( x + h ) с точностью до первой степени h ..., словом, повторили бы все то, что мы намерены сделать с η.

Итак, идея наша заключается в том, что мы подставляем x ( t )= _x ( t )+η( t ) в формулу для действия

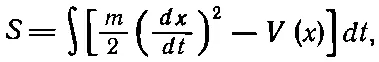
где через V ( x ) обозначена потенциальная энергия. Производная dx / dt — это, естественно, производная от _x ( t ) плюс производная от η( t ), так что для действия я получаю такое выражение:

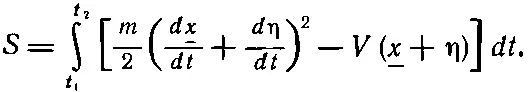
Теперь это нужно расписать подетальней. Для квадратичного слагаемого я получу

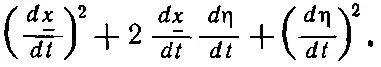
Но постойте-ка! Ведь мне не нужно заботиться о порядках выше первого. Я могу убрать все слагаемые, в которых есть η 2и высшие степени, и ссыпать их в ящик под названием «второй и высшие порядки». Из этого выражения туда попадет только одна вторая степень, но из чего-то другого могут войти и высшие. Итак, часть, связанная с кинетической энергией, такова:

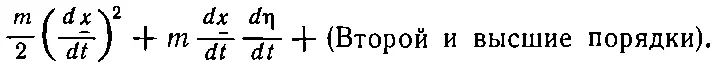
Дальше нам нужен потенциал V в точках _ x +η. Я считаю η малой и могу разложить V ( x ) в ряд Тэйлора. Приближенно это будет V ( _x ); в следующем приближении (из-за того, что здесь стоят обычные производные) поправка равна η, умноженной на скорость изменения V по отношению к x; и т. д.:

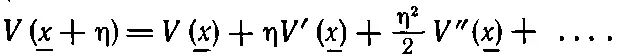
Для экономии места я обозначил через V производную F по х . Слагаемое с η 2и все, стоящие за ним, попадают в категорию «второй и высшие порядки». И о них больше нечего беспокоиться. Объединим все, что осталось:

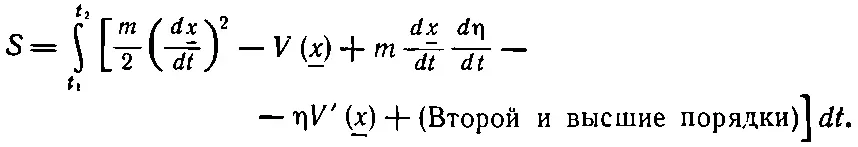
Если мы теперь внимательно взглянем на это, то увидим, что два первых написанных здесь члена отвечают тому действию _S , которое я написал бы для искомого истинного пути _х . Я хочу сосредоточить ваше внимание на изменении S , т. е. на разности между S и тем _S , которое получилось бы для истинного пути. Эту разность мы будем записывать как δ S и назовем ее вариацией S . Отбрасывая «второй и высшие порядки», получаем для δS

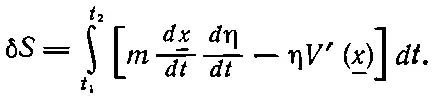
Теперь задача выглядит так. Вот передо мной некоторый интеграл. Я не знаю еще, каково это _х , но я твердо знаю, что, какую η я ни возьму, этот интеграл должен быть равен нулю. «Ну что ж,— подумаете вы,— единственная возможность для этого — это чтобы множитель при η был равен нулю». Но как быть с первым слагаемым, где есть d η/ dt ? Вы скажете: «Если η обращается в ничто, то и ее производная такое же ничто; значит, коэффициент при d η/ dt должен тоже быть нулем». Ну это не совсем верно. Это не совсем верно потому, что между отклонением η и его производной имеется связь; они не полностью независимы, потому что η(t) должно быть нулем и при t 1и при t 2.

При решении всех задач вариационного исчисления всегда пользуются одним и тем же общим принципом. Вы чуть сдвигаете то, что хотите варьировать (подобно тому, как это сделали мы, добавляя η), бросаете взгляд на члены первого порядка, затем расставляете все так, чтобы получился интеграл в таком виде: «сдвиг (η), умноженный на что получится», но чтобы в нем не было никаких производных от η (никаких d η/ dt ). Непременно нужно так все преобразовать, чтобы осталось «нечто», умноженное на η. Сейчас вы поймете, отчего это так важно. (Существуют формулы, которые подскажут вам, как в некоторых случаях можно это проделать без каких-либо выкладок; но они не так уж общи, чтобы стоило заучивать их; лучше всего проделывать выкладки так, как это делаем мы.)

Как же я могу переделать член d η/ dt , чтобы в нем появилось η? Я могу добиться этого, интегрируя по частям. Оказывается, что в вариационном исчислении весь фокус в том и состоит, чтобы расписать вариацию S и затем проинтегрировать по частям так, чтобы производные от η исчезли. Во всех задачах, в которых появляются производные, проделывается такой же фокус.

Припомните общий принцип интегрирования по частям. Если у вас есть произвольная функция f, умноженная на d η/ dt и проинтегрированная по t , то вы расписываете производную от η f :

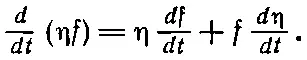
В интересующем вас интеграле стоит как раз последнее слагаемое, так что

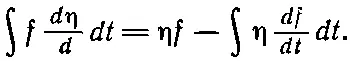
В нашей формуле для δS за функцию f принимается произведение m на d_x / dt ; поэтому я получаю для δ S выражение