Ричард Фейнман - Том 2. Электромагнетизм и материя

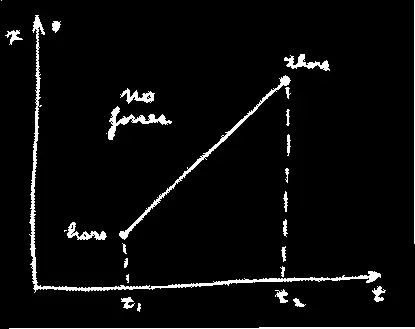
здесь * сил нет * там

Предмет же, подброшенный в поле тяжести вверх, сперва поднимается быстро, а потом все медленнее. Происходит это потому, что он обладает и потенциальной энергией, а наименьшего значения должна достигать разность между кинетической и потенциальной энергиями. Раз потенциальная энергия возрастает по мере подъема, то меньшая разность получится, если как можно быстрее достичь тех высот, где потенциальная энергия велика. Тогда, вычтя из кинетической энергии этот высокий потенциал, мы добьемся уменьшения среднего. Так что выгоднее такой путь, который идет вверх и поставляет добрый отрицательный кусок за счет потенциальной энергии.

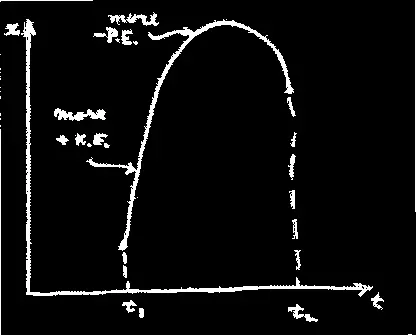
больше + к. э . * болъше - п. э .

Но, с другой стороны, нельзя ни двигаться слишком быстро, ни подняться слишком высоко, потому что на это потребуется чересчур много кинетической энергии. Надо двигаться достаточно быстро, чтобы подняться и спуститься за определенное время, имеющееся в твоем распоряжении. Так что не следует стараться взлететь слишком высоко, а просто надо достичь какого-то разумного уровня. В итоге оказывается, что решение есть своего рода равновесие между желанием раздобыть как можно больше потенциальной энергии и желанием как можно сильней уменьшить количество кинетической энергии — это стремление добиться максимального уменьшения разности кинетической и потенциальной энергий».

Вот и все, что сказал мне мой учитель, потому что он был очень хороший учитель и знал, когда пора остановиться. Сам я, увы, не таков. Мне трудно остановиться вовремя. И поэтому вместо того, чтобы просто разжечь в вас интерес своим рассказом, я хочу запугать вас, хочу, чтобы вам стало тошно от сложности жизни,— попробую доказать то, о чем я рассказал. Математическая задача, которую мы будем решать, очень трудна и своеобразна. Имеется некоторая величина S , называемая действием . Она равна кинетической энергии минус потенциальная, проинтегрированная по времени:

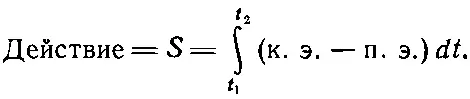
Не забудьте, что и п. э. и к. э.— обе функции времени. Для любого нового мыслимого пути это действие принимает свое определенное значение. Математическая задача состоит в том, чтобы определить, для какой кривой это число меньше, чем для других.

Вы скажете: «О, это просто обычный пример на максимум и минимум. Надо подсчитать действие, продифференцировать его и найти минимум».

Но погодите. Обычно у нас бывает функция какой-то переменной и нужно найти значение переменной , при котором функция становится наименьшей или наибольшей. Скажем, имеется стержень, нагретый посредине. По нему растекается тепло и в каждой точке стержня устанавливается своя температура. Нужно найти точку, где она выше всего. Но у нас речь идет совсем об ином — каждому пути в пространстве отвечает свое число, и предполагается найти тот путь , для которого это число минимально. Это совсем другая область математики. Это не обычное исчисление, а вариационное (так его называют).

В этой области математики имеется много своих задач. Скажем, окружность обычно определяют как геометрическое место точек, расстояния которых от данной точки одинаковы, но окружность можно определить и иначе: это та из кривых данной длины , которая ограничивает собою наибольшую площадь. Любая другая кривая такого же периметра ограничивает площадь меньшую, чем окружность. Так что если поставить задачу: найти кривую данного периметра, ограничивающую наибольшую площадь, то перед нами будет задача из вариационного исчисления, а не из того исчисления, к которому вы привыкли.

Итак, мы хотим взять интеграл по пути, пройденному телом. Сделаем это так. Все дело в том, чтобы вообразить себе, что существует истинный путь и что любая другая кривая, которую мы проведем,— не настоящий путь, так что если подсчитать для нее действие, то получится число, превышающее то, которое мы получим для действия, соответствующего настоящему пути.

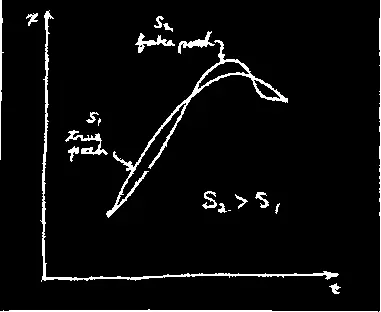
верный путь * неверный путь

Итак, задача: найти истинный путь. Где он пролегает? Один из способов, конечно, мог бы состоять в том, чтобы подсчитать действие для миллионов и миллионов путей и потом посмотреть, при каком пути это действие наименьшее. Вот тот путь, при котором действие минимально, и будет настоящим.

Такой способ вполне возможен. Однако можно сделать проще. Если имеется величина, обладающая минимумом (из обычных функций, скажем, температура), то одно из свойств минимума состоит в том, что при удалении от него на расстояние первого порядка малости функция отклоняется от минимального своего значения только на величину второго порядка. А в любом другом месте кривой сдвиг на малое расстояние изменяет значение функции тоже на величину первого порядка малости. Но в минимуме легкие уходы в сторону в первом приближении не приводят к изменению функции.

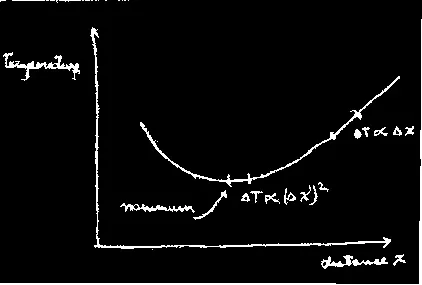
температура * минимум * расстояние

Это-то свойство мы и собираемся использовать для расчета настоящего пути. Если путь правильный, то кривая, чуть-чуть отличная от него, не приведет в первом приближении к изменению в величине действия. Все изменения, если это был действительно минимум, возникнут только во втором приближении.

Это легко доказать. Если при каком-то отклонении от кривой возникают изменения в первом порядке, то эти изменения в действии пропорциональны отклонению. Они, по всей вероятности, увеличат действие; иначе это не был бы минимум. Но раз изменения пропорциональны отклонению, то перемена знака отклонения уменьшит действие. Выходит, что при отклонении и одну сторону действие возрастает, а при отклонении в обратную сторону — убывает. Единственная возможность того, чтобы это действительно был минимум,— это чтобы в первом приближении никаких изменений не происходило и изменения были бы пропорциональны квадрату отклонения от настоящего пути.

Итак, мы пойдем по следующему пути: обозначим через _x ( t ) (с чертой внизу) истинный путь — тот, который мы хотим найти. Возьмем некоторый пробный путь x ( t ), отличающийся от искомого на небольшую величину, которую мы обозначим η(t).