Ричард Фейнман - Том 2. Электромагнетизм и материя

Мы можем показать, что оба эти утверждения относительно электростатики эквивалентны. Предположим, что мы выбрали произвольную функцию φ. Мы хотим показать, что когда в качестве φ мы возьмем правильное значение потенциала _φ плюс малое отклонение f, то в первом порядке малости изменение в U *будет равно нулю. Так что мы пишем

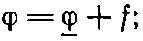
здесь _φ — это то, что мы ищем; но мы проварьируем _φ, чтобы увидеть, каким он должен быть для того, чтобы вариация U *оказалась первого порядка малости. В первом члене U *нам нужно написать

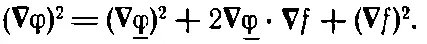
Единственный член первого порядка, который будет меняться, таков:

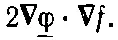
Во втором члене U *подынтегральное выражение примет вид

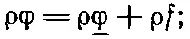
изменяющаяся часть здесь равна ρf. Оставляя только меняющиеся члены, получим интеграл

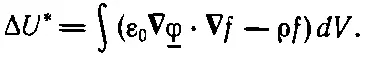
Дальше, руководствуясь нашим старым общим правилом, мы должны очистить интеграл от всех производных по f. Посмотрим, что это за производные. Скалярное произведение равно

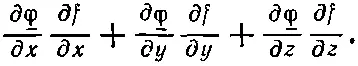
Это нужно проинтегрировать по x, у и по z. И здесь напрашивается тот же фокус: чтобы избавиться от df / dx , мы проинтегрируем по x по частям. Это приведет к добавочному дифференцированию _φ по x. Это та же основная идея, с помощью которой мы избавились от производных по t . Мы пользуемся равенством

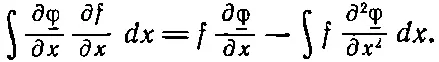
Проинтегрированный член равен нулю, так как мы считаем f равным нулю на бесконечности. (Это отвечает обращению η в нуль при t 1и t 2. Так что наш принцип более точно формулируется следующим образом: U *для правильного φ меньше, чем для любого другого ого мы получаем следующее дифференциальное φ( х, у , z), обладающего теми же значениями на бесконечности.) Затем мы проделаем то же с у и с z. Наш интеграл Δ U *обратится в

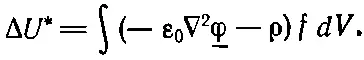
Чтобы эта вариация была равна нулю при любом произвольном f, коэффициент при f должен быть равен нулю. Значит,

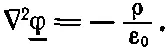
Мы вернулись к нашему старому уравнению. Значит, наше «минимальное» предложение верно. Его можно обобщить, если слегка изменить выкладки. Вернемся назад и проинтегрируем по частям, не расписывая все покомпонентно. Начнем с того, что напишем следующее равенство:

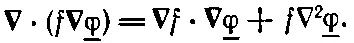
Продифференцировав левую часть, я могу показать, что она в точности равна правой. Это уравнение подходит для того, чтобы провести интегрирование но частям. В нашем интеграле Δ U *мы заменяем ∇_φ· ∇f на —f ∇ 2_φ+ ∇·(f ∇_φ) и затем интегрируем это по объему. Член с дивергенцией после интегрирования по объему заменяется интегралом по поверхности:

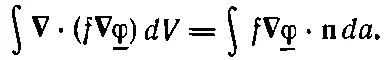
А поскольку мы интегрируем по всему пространству, то поверхность в этом интеграле лежит на бесконечности. Значит, f=0, и мы получаем прежний результат.

Только теперь мы начинаем понимать, как решать задачи, в которых мы не знаем , где расположены все заряды. Пусть мы имеем проводники, на которых как-то распределены заряды. Если потенциалы на всех проводниках зафиксированы, то наш принцип минимума все еще разрешается применять. Интегрирование в U *мы проведем только по области, лежащей снаружи всех проводников. Но раз мы не можем на проводниках менять _φ, то на их поверхности f=0, и поверхностный интеграл

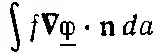
тоже равен нулю. Остающееся объемное интегрирование нужно проделывать только в промежутках между проводниками.

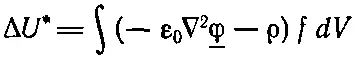
И мы, конечно, снова получаем уравнение Пуассона

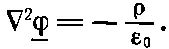
Мы, стало быть, показали, что наш первоначальный интеграл U *достигает минимума и тогда, когда он вычисляется в пространстве между проводниками, каждый из которых находится при фиксированном потенциале [это значит, что каждая пробная функция φ( х, у, z ) должна равняться заданному потенциалу проводника, когда ( х, у, z ) — точки поверхности проводника]. Существует интересный частный случай, когда заряды расположены только на проводниках. Тогда

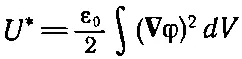
и наш принцип минимума говорит нам, что в случае, когда у каждого проводника есть свой заранее заданный потенциал, потенциалы в промежутках между ними пригоняются так, что интеграл U *оказывается как можно меньше. А что это за интеграл? Член ∇φ — это электрическое поле. Значит, интеграл — это электростатическая энергия. Правильное поле и есть то единственное, которое из всех полей, получаемых как градиент потенциала, отличается наименьшей полной энергией.

Я хотел бы воспользоваться этим результатом, чтобы решить какую-нибудь частную задачу и показать вам, что все эти вещи имеют реальное практическое значение. Предположим, что я взял два проводника в форме цилиндрического конденсатора.

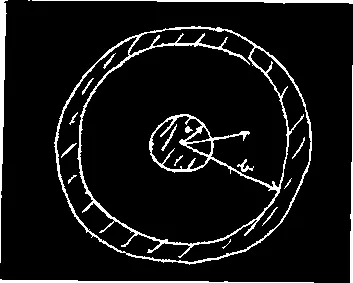
У внутреннего проводника потенциал равен, скажем, V , а у внешнего— нулю. Пусть радиус внутреннего проводника будет равен а , а внешнего — b. Теперь мы можем предположить, что распределение потенциалов между ними — любое . Но если мы возьмем правильное значение φ и вычислим (ε 0/2)∫(∇_φ) 2 dV , то должна получиться энергия системы 1/ 2CV 2. Так что с помощью нашего принципа можно подсчитать и емкость С . Если же мы возьмем неправильное распределение потенциала и попытаемся этим методом прикинуть емкость конденсатора, то придем к чересчур большому значению емкости при фиксированном V . Любой предполагаемый потенциал φ, не точно совпадающий с истинным его значением, приведет и к неверной величине С , большей, чем нужно. Но если неверно выбранный потенциал φ является еще грубым приближением, то емкость С получится уже с хорошей точностью, потому что погрешность в С — величина второго порядка по сравнению с погрешностью в φ.