Ричард Фейнман - Том 2. Электромагнетизм и материя

Предположим, что мне неизвестна емкость цилиндрического конденсатора. Тогда, чтобы узнать ее, я могу воспользоваться этим принципом. Я просто буду испытывать в качестве потенциала разные функции φ до тех пор, пока не добьюсь наинизшего значения С . Допустим, к примеру, что я выбрал потенциал, отвечающий постоянному полю. (Вы, конечно, знаете, что на самом деле поле здесь не постоянно; оно меняется как 1/r) Если поле постоянно, то это означает, что потенциал линейно зависит от расстояния. Чтобы напряжение на проводниках было каким нужно, функция φ должна иметь вид

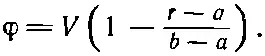
Эта функция равна V при r= а , нулю при r=b, а между ними имеется постоянный наклон, равный — V /( b - а ). Значит, чтобы определить интеграл U *, надо только помножить квадрат этого градиента на ε 0/2 и проинтегрировать по всему объему. Проведем этот расчет для цилиндра единичной длины. Элемент объема при радиусе r равен 2π rdr . Проводя интегрирование, я нахожу, что моя первая проба дает такую емкость:

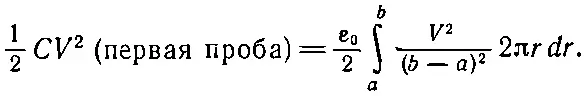
Интеграл здесь просто равен

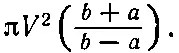
Так я получаю формулу для емкости, которая хотя и неправильна, но является каким-то приближением:

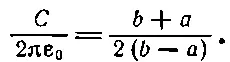
Конечно, она отличается от правильного ответа C=2πε 0/ln( b / a ), но в общем-то она не так уж плоха. Давайте попробуем сравнить ее с правильным ответом для нескольких значений b / а . Вычисленные мною числа приведены в следующей таблице

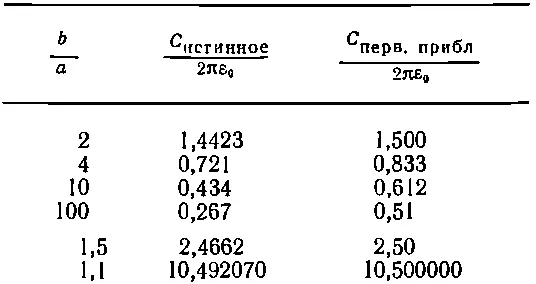
Даже когда b / a =2 (а это приводит уже к довольно большим отличиям между постоянным и линейным полем), я все еще получаю довольно сносное приближение. Ответ, конечно, как и ожидалось, чуть завышен. Но если тонкую проволочку поместить внутри большого цилиндра, то все выглядит уже гораздо хуже. Тогда поле изменяется очень сильно и замена его постоянным полем ни к чему хорошему не приводит. При b/а=100 мы завышаем ответ почти вдвое. Для малых b/ а положение выглядит намного лучше. В противоположном пределе, когда промежуток между проводниками не очень широк (скажем, при b/а=1,1), постоянное поле оказывается весьма хорошим приближением, оно дает значение С с точностью до десятых процента.

А теперь я расскажу вам, как усовершенствовать этот расчет. (Ответ для цилиндра вам, разумеется, известен , но тот же способ годится и для некоторых других необычных форм конденсаторов, для которых правильный ответ вам может быть и не известен.) Следующим шагом будет подыскание лучшего приближения для неизвестного нам истинного потенциала φ. Скажем, можно испытать константу плюс экспоненту φ и т. д. Но как вы узнаете, что у вас получилось лучшее приближение, если вы не знаете истинного φ? Ответ : Подсчитайте С ; чем оно ниже, тем к истине ближе. Давайте проверим эту идею. Пусть потенциал будет не линейным, а, скажем, квадратичным по r, а электрическое поле не постоянным, а линейным. Самая общая квадратичная форма, которая обращается в φ=0 при r= b и в φ=V при r=а, такова:

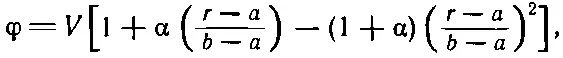
где α — постоянное число. Эта формула чуть сложнее прежней. В нее входит и квадратичный член, и линейный. Из нее очень легко получить поле. Оно равно просто

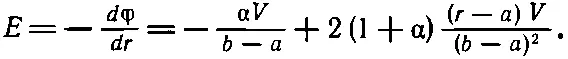
Теперь это нужно возвести в квадрат и проинтегрировать по объему. Но погодите минутку. Что же мне принять за α? За φ я могу принять параболу, но какую? Вот что я сделаю: подсчитаю емкость при произвольном α. Я получу

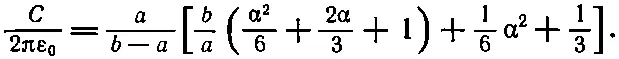
Это выглядит малость запутанно, но так уж выходит после интегрирования квадрата поля. Теперь я могу выбирать себе а. Я знаю, что истина лежит ниже, чем все, что я собираюсь вычислить. Что бы я ни поставил вместо α, ответ все равно получится слишком большим. Но если я продолжу свою игру с α и постараюсь добиться наинизшего возможного значения С , то это наинизшее значение будет ближе к правде, чем любое другое значение. Следовательно, мне теперь надо подобрать α так, чтобы значение С достигло своего минимума. Обращаясь к обычному дифференциальному исчислению, я убеждаюсь, что минимум С будет тогда, когда α=-2 b /( b + а ). Подставляя это значение в формулу, я получаю для наименьшей емкости

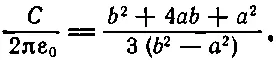
Я прикинул, что дает эта формула для С при различных значениях b / а . Эти числа я назвал С (квадратичные). Привожу таблицу, в которой сравниваются С (квадратичные) с С (истинными).

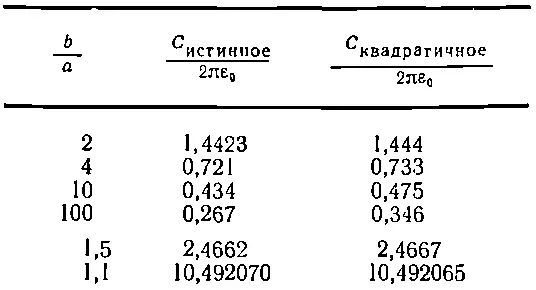
Например, когда отношение радиусов равно 2:1, я получаю 1,444. Это очень хорошее приближение к правильному ответу, 1,4423. Даже при больших b / а приближение остается довольно хорошим — оно намного лучше первого приближения. Оно остается сносным (завышение только на 10%) даже при b / а =10:1. Большое расхождение наступает только при отношении 100:1. Я получаю С равным 0,346 вместо 0,267. С другой стороны, для отношения радиусов 1,5 совпадение превосходное, а при b / a =1,1 ответ получается 10,492065 вместо положенного 10,492070. Там, где следует ожидать хорошего ответа, он оказывается очень и очень хорошим.

Я привел все эти примеры, во-первых, чтобы продемонстрировать теоретическую ценность принципа минимального действия и вообще всяких принципов минимума, и, во-вторых, чтобы показать вам их практическую полезность, а вовсе не для того, чтобы подсчитать емкость, которую мы и так великолепно знаем. Для любой другой формы вы можете испробовать приближенное поле с несколькими неизвестными параметрами (наподобие α) и подогнать их под минимум. Вы получите превосходные численные результаты в задачах, которые другим способом не решаются.