Ричард Фейнман - Том 2. Электромагнетизм и материя

Можно было бы прямо рассмотреть решение волнового уравнения для какой-нибудь из электромагнитных величин. Вместо этого мы начнем прямо с начала, с уравнений Максвелла для пустого пространства, и вы убедитесь в их тесной связи с электромагнитными волнами. Так что мы отправляемся от уравнений (20.1), полагая, что в них токи и заряды равны нулю. Они обращаются в

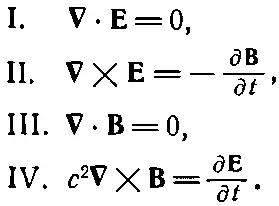(20.12)

Распишем первое уравнение покомпонентно:

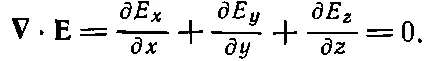(20.13)

Мы предположили, что по у и z поле не меняется, так что два последних члена равны нулю. Тогда, согласно (20.13),

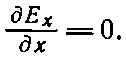(20.14)

Решением его является постоянное в пространстве Е х (компонента электрического поля в направлении х ). Взглянув на уравнение IV в (20.12) и полагая, что Втоже не изменяется вдоль y и z , вы убедитесь, что Е х постоянно и во времени. Таким полем может оказаться постоянное поле от какого-то заряженного конденсатора вдали от этого конденсатора. Нас сейчас не занимают такие неинтересные статические поля; мы интересуемся лишь динамически изменчивыми полями. А для динамических полей Е х =0.

Итак, мы пришли к важному результату о том, что при распространении плоских волн в произвольном направлении электрическое поле должно располагаться поперек направления своего распространения . Конечно, у него еще остается возможность каким-то сложным образом изменяться по координате х .

Поперечное поле Еможно всегда разбить на две компоненты, скажем на у и z . Так что сначала разберем случай наличия у электрического поля только одной поперечной компоненты. Для начала возьмем электрическое поле, направленное по у , т. е. с нулевой z-компонентой. Ясно, что, решив эту задачу, мы всегда сможем разобрать и тот случай, когда электрическое поле всюду направлено по z. Общее решение можно всегда представить в виде суперпозиции двух таких полей.

Какими простыми стали теперь наши уравнения! Теперь единственная ненулевая компонента электрического поля — это Е у , и все производные (кроме производных по х ) тоже равны нулю. Остатки уравнений Максвелла выглядят чрезвычайно просто.

Рассмотрим теперь второе из уравнений Максвелла [т. е. II из (20.12)]. Расписав компоненты rot E, получаем

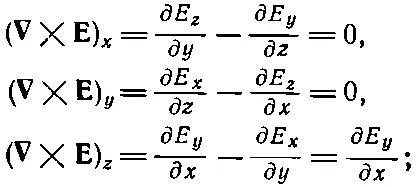
здесь x-компонента ∇× Eравна нулю, потому что равны нулю производные по у и z; y-компонента тоже равна нулю: первый член потому, что все производные по z равны нулю, а второй потому, что E z =0. Единственная не равная нулю компонента rot E— это z-компонента, она равна ∂ E у /∂ x . Полагая, что три компоненты ∇× Eравны соответствующим компонентам —∂ B/∂ t , мы заключаем, что

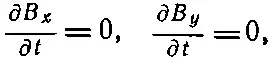(20.15)

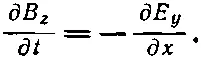(20.16)

Поскольку временные производные как x-компоненты магнитного поля, так и y-компоненты магнитного поля равны нулю, то обе эти компоненты суть попросту постоянные поля и отвечают найденным раньше магнитостатическим решениям. Ведь кто-то мог оставить постоянный магнит возле того места, где распространяются волны. Мы будем игнорировать эти постоянные поля и положим В х и В y равными нулю.

Кстати, о равенстве нулю x-компонент поля Вмы должны были бы заключить и по другой причине. Поскольку дивергенция Вравна нулю (по третьему уравнению Максвелла), то мы, прибегая при рассмотрении электрического поля к тем же доводам, что и выше, должны были бы прийти к выводу, что продольная компонента магнитного поля не может изменяться вдоль х . А раз мы такими однородными полями в наших волновых решениях пренебрегаем, то нам следовало бы положить В х равным нулю. В плоских электромагнитных волнах поле В, равно как и поле Е, должно быть направлено поперек направления распространения самих волн.

Равенство (20.16) дает нам добавочное утверждение о том, что если электрическое поле имеет только y -компоненту, то магнитное поле имеет только z -компоненту. Значит, Еи В перпендикулярны друг другу. Именно это и наблюдалось в той волне особого типа, которую мы уже рассмотрели.

Теперь мы готовы использовать последнее из уравнений Максвелла для пустого пространства [т. е. IV из (20.12)]. Расписывая покомпонентно, имеем

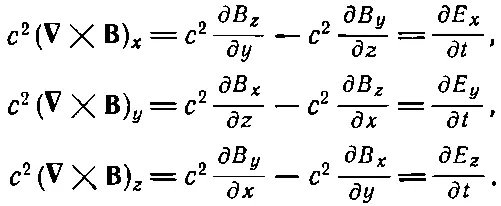(20.17)

Из шести производных от компонент Втолько ∂ B z /∂ x не равна нулю. Так что три уравнения просто дают

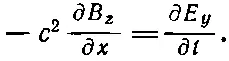(20.18)

Итог всей нашей деятельности состоит в том, что отличны от нуля только по одной компоненте электрического и магнитного полей и эти компоненты обязаны удовлетворять уравнениям (20.16) и (20.18). Эти два уравнения можно объединить в одно, если первое из них продифференцировать по х, а второе— по t ; тогда левые стороны уравнений совпадут (с точностью до множителя с 2). И мы обнаруживаем, что Е y подчиняется уравнению

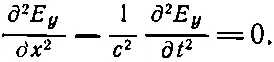(20.19)

Мы уже встречали это дифференциальное уравнение, когда изучали распространение звука. Это волновое уравнение для одномерных волн.

Заметьте, что в процессе вывода мы получили больше , чем содержится в (20.11). Уравнения Максвелла дали нам информацию и о том, что у электромагнитных волн есть только компоненты поля, расположенные под прямым углом к направлению распространения волн.

Вспомним все, что нам известно о решениях одномерного волнового уравнения. Если какая-то величина ψ удовлетворяет одномерному волновому уравнению

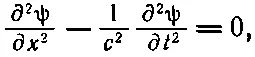(20.20)

то одним из возможных решений является функция ψ( x, t ), имеющая вид

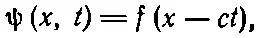(20.21)