Ричард Фейнман - Том 2. Электромагнетизм и материя

т. е. функция одной - единственной переменной ( x - ct ). Функция f ( x - ct ) представляет собой «жесткое» образование вдоль оси х , которое движется по направлению к положительным х со скоростью с (фиг. 20.4).

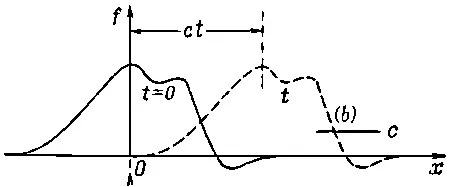
Фиг. 20.4. Функция f(x-ct) представляет неизменный «контур», движущийся в направлении возрастания х со скоростью с.

Так, если максимум функции f приходится на нулевое значение аргумента, то при t =0 максимум ψ оказывается при x =0. В более поздний момент, скажем при t =10, максимум ψ окажется в точке х =10 с . Когда время движется, максимум тоже движется в сторону возрастания х со скоростью с. Порой удобнее считать, что решение одномерного волнового уравнения является функцией от ( t - х / с ). Однако в сущности это одно и то же, потому что любая функция от ( t - х / с )— это также функция от ( x - ct ):

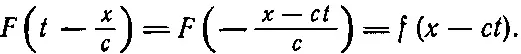
Покажем, что f ( x - ct ) действительно есть решение волнового уравнения. Поскольку f зависит лишь от одной переменной — переменной ( x - ct ), то мы будем через f ' обозначать производную f по этой переменной, а через f "— вторую производную. Дифференцируя (20.21) по х , получаем

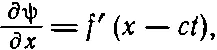
потому что производная от ( x - ct ) по x равна единице. Вторая производная ψ по x равна

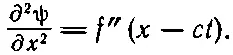(20.22)

А производные ψ по t дают

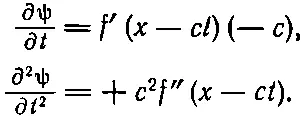(20.23)

Мы убеждаемся, что ψ действительно удовлетворяет одномерному волновому уравнению.

Вы недоумеваете: «Откуда же вы взяли, что решением волнового уравнения является f ( x - ct )? Мне эта проверка задним числом совсем не нравится. Нет ли прямого пути отыскать решение?» Хорошо, вот вам прямой путь: знать решение. Можно, конечно, «испечь» по всей науке прямые математические аргументы, тем более, что мы знаем, каким должно быть решение, но с таким простым, как у нас, уравнением игра не стоит свеч. Со временем вы сами дойдете до того, что, как только; увидите уравнение (20.20), тут же будете представлять себе f ( x - ct )=ψ в качестве решения. (Подобно тому, как сейчас при виде интеграла от x 2 dx у вас сразу всплывает ответ x 3/3.)

На самом деле вы должны представлять себе немножко больше. Решением является не только любая функция от ( x - ct ), но и функция от ( х + сt ). Из-за того, что в волновом уравнении с встречается только в виде с 2, изменение знака с ничего не меняет. И действительно, самое общее решение одномерного волнового уравнения — это сумма двух произвольных функций, одной от аргумента ( x - ct ), а другой от ( x + ct ):

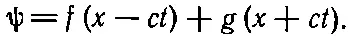
(20.24)

Первое слагаемое дает волну, движущуюся по направлению к положительным х , второе — произвольную волну, бегущую к отрицательным х . Общее решение получается наложением двух таких волн, существующих одновременно.

Следующий забавный вопрос решите сами. Возьмем функцию ψ в виде

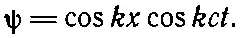
Эта функция не имеет вида f(x- ct ) или g ( x + ct ). Но прямой подстановкой в (20.20) легко убедиться, что она удовлетворяет волновому уравнению. Но как же мы тогда смеем говорить, что общее решение имеет вид (20.24)?

Применяя эти выводы о решении волнового уравнения к y -компоненте электрического поля Е у , мы заключаем, что Е y может меняться по х произвольным образом. Всякое поле, которое существует в самом деле, можно всегда рассматривать как сумму двух картин. Одна волна плывет через пространство в каком-то направлении со скоростью с , причем связанное с нею магнитное поле перпендикулярно к электрическому; другая волна бежит в противоположном направлении с той же скоростью. Такие волны отвечают хорошо нам известным электромагнитным волнам — свету, радиоволнам, инфракрасному излучению, ультрафиолету, рентгеновским лучам и т. д. Мы уже изучали очень подробно излучение света. Так как все, чему мы тогда научились, применимо к любым электромагнитным волнам, то теперь нет нужды рассматривать подробно поведение этих волн.

Пожалуй, стоит лишь сделать несколько замечаний о поляризации электромагнитных волн. Раньше мы решили рассмотреть частный случай электрического поля с одной только y-компонентой. Имеется, конечно, и другое решение для волн, бегущих в направлении + х или - х , т. е. решение, при котором электрическое поле обладает одной лишь z-компонентой. Так как уравнения Максвелла линейны, общее решение для одномерных волн, распространяющихся в направлении х , есть сумма волн Е y и волн Е z . Общее решение суммируется следующими формулами:

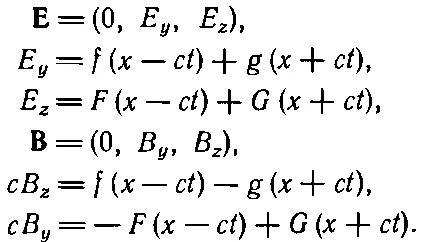(20.25)

У подобных электромагнитных волн направление вектора Ене неизменно: оно как-то произвольно смещается по спирали в плоскости yz . Но в каждой точке магнитное поле всегда перпендикулярно к электрическому и к направлению распространения.

Если присутствуют только волны, бегущие в одном направлении (скажем, в положительном направлении х ), то имеется простое правило, говорящее об относительной ориентации электрического и магнитного полей. Правило состоит в том, что векторное произведение Е× B(которое, как известно, является вектором, поперечным и к Е, и к В) указывает направление, куда бежит волна. Если Есовмещать с Вправым поворотом, то вектор поворота показывает направление вектора скорости волны. (Позже мы увидим, что вектор Е× Bимеет особый физический смысл: это вектор, описывающий течение энергии в электромагнитном поле.)

А теперь обратимся к трехмерным волнам. Мы уже знаем, что вектор Еудовлетворяет волновому уравнению. К тому же выводу легко прийти, отправляясь прямо от уравнений Максвелла. Предположим, что мы исходим из уравнения