Ричард Фейнман - Том 2. Электромагнетизм и материя

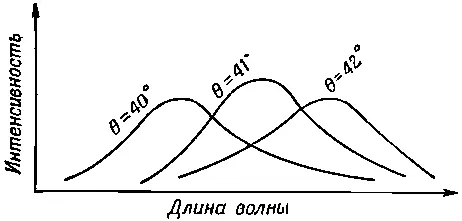
Фиг. 20.5. Зависимость интенсивности электромагнитных волн от длины волны под тремя углами (отсчитываемыми от направления, противоположного направлению на Солнце). Доступно наблюдению лишь в определенных метеорологических условиях.

Но находите ли вы график, приведенный на фиг. 20.5, восхитительным? В нем ведь содержится существенно больше различных деталей, чем мы в состоянии постичь, когда видим радугу: наши глаза не могут схватить доподлинную форму спектра. А вот глазам радуга все же кажется восхитительной. Хватает ли у вас воображения, чтобы в спектральных кривых увидеть всю ту красоту, которую мы видим, смотря на радугу? У меня — нет.

Но представим себе, что у меня имеется график зависимости коэффициента отражения кристаллов хлористого натрия от длины волны в инфракрасном участке спектра и от угла. Я могу вообразить себе, как это представилось бы моим глазам, обладай они способностью видеть в инфракрасном свете. Должно быть, это был бы какой-то яркий, насыщенный «зеленый цвет», на который накладывались бы отражения от поверхностей «металлически-красных» тонов. Это выглядело бы поистине великолепно, но я не знаю, способен ли я, взглянув на график коэффициента отражения NaCl, снятый на каком-то приборе, сказать, что он столь же прелестен.

Но, с другой стороны, хоть мы и не можем видеть красоту тех или иных частных измерений, мы можем утверждать, что постигаем своеобразную красоту уравнений, описывающих всеобщие физические законы. Например, в волновом уравнении (20.9) очень красива та правильность, с какой в нем расположены х, у, z и t . И эта приятная симметрия появления х , у, z, t намекает на ту величественную красоту, которая таится в четырех равнозначных координатах, в возможности того, что у пространства есть четырехмерная симметрия, в возможности проанализировать ее и развить специальную теорию относительности. Так что существует еще интеллектуальная красота, ассоциируемая с уравнениями.

Мы видели, что существуют решения волнового уравнения, отвечающие плоским волнам, и что любая электромагнитная волна может быть описана как суперпозиция многих плоских волн. В определенных случаях, однако, удобнее описывать волновое поле в другой математической форме. Я хотел бы сейчас разобрать теорию сферических волн — волн, которые соответствуют сферическим поверхностям, расходящимся из некоторого центра. Когда вы бросаете камень в пруд, то по водной глади побежит рябь в виде круговых волн — это двумерные волны. Сферические волны похожи на них, только распространяются они во всех трех измерениях.

Прежде чем начать описание сферических волн, немного займемся математикой. Пусть имеется функция, зависящая только от радиального расстояния r точки от начала координат, иными словами, сферически симметричная функция. Обозначим ее ψ(r), где под r подразумевается

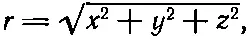
т. е. расстояние от начала координат. Чтобы узнать, какие функции ψ(r) удовлетворяют волновому уравнению, нам понадобится выражение для лапласиана ψ. Значит, нам нужно найти сумму вторых производных ψ по х , по у и по z. Через ψ'(r) мы обозначим первую производную ψ по r, а через ψ"(r) — вторую. Сначала найдем производные по х . Первая производная равна

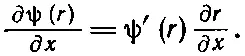
Вторая производная по х равна

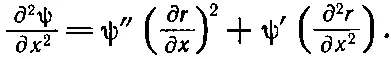
Частные производные r по x можно получить из

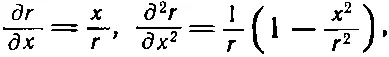
так что вторая производная ψ по x принимает вид

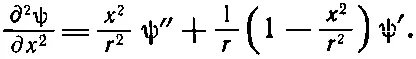(20.28)

Точно так же и

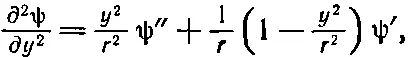(20.29)

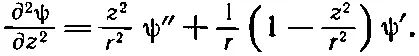(20.30)

Лапласиан равен сумме этих трех производных. Вспоминая, что x 2+y 2+z 2=r 2, получаем

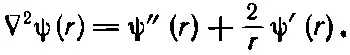(20.31)

Часто бывает удобнее записывать уравнение в следующей форме:

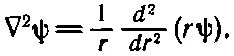(20.32)

Проделав дифференцирование, указанное в (20.32), вы убедитесь, что правая часть здесь та же, что и в (20.31).

Если мы хотим рассматривать сферически симметричные поля, которые могут распространяться как сферические волны, то величины, описывающие поля, должны быть функцией как r, так и t . Предположим, что нам нужно знать, какие функции ψ(r, t ) являются решениями трехмерного волнового уравнения

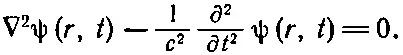(20.33)

Поскольку ψ( r, t ) зависит от пространственных координат только через r, то в качестве лапласиана можно использовать выражение (20.32). Но для точности, поскольку ψ зависит также и от t , нужно дифференцирование по r записывать в виде частной производной. Волновое уравнение обращается в

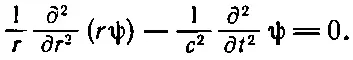
Его и предстоит нам решать. Оно выглядит сложнее, чем в случае плоских волн. Но заметьте, что если умножить это уравнение на r, то получится

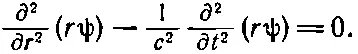(20.34)

Это уравнение говорит нам, что функция rψ удовлетворяет одномерному волновому уравнению по переменной r. Используя часто подчеркивавшийся нами общий принцип, что у одних и тех же уравнений и решения одни и те же, мы приходим к выводу, что если rψ окажется функцией одного только ( r - ct ), то оно явится решением уравнения (20.34). Итак, мы обнаруживаем, что сферические волны обязаны иметь вид

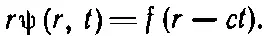
Или, как мы видели раньше, можно в равной степени считать rψ имеющим форму