Ричард Фейнман - Том 2. Электромагнетизм и материя

В гл. 18 мы установили, что уравнения Максвелла можно решать подстановкой

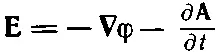(21.2)

и

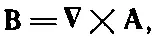(21.3)

где φ и Аобязаны удовлетворять уравнениям

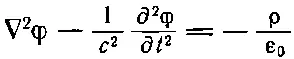(21.4)

и

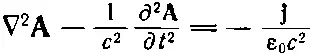(21.5)

и, кроме того, условию

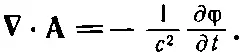(21.6)

Найдем теперь решение уравнений (21.4) и (21.5). Для этого надо уметь решать уравнение

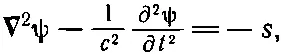(21.7)

где величина s (которая называется источником) известна. Ясно, что для уравнения (21.4) s соответствует ρ/ε 0, а ψ — это φ, а для уравнения (21.5) s соответствует j x/ε 0с 2, если ψ — это А х , и т. д. Но нас интересует чисто математическая задача решения (21.7) безотносительно к тому, каков физический смысл ψ и s.

Там, где ρ и jравны нулю (это место называется «пустотой»), там потенциалы φ и Аи поля Еи Вудовлетворяют трехмерному волновому уравнению без источников; математическая форма этого уравнения такова:

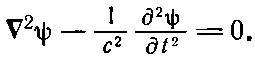(21.8)

В гл. 20 мы видели, что решения этого уравнения могут представлять волны разных сортов: плоские волны, бегущие в x-направлении ψ=f(t-x/с); плоские волны, бегущие вдоль у или вдоль z или в любом другом направлении; сферические волны вида

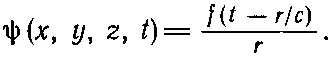(21.9)

(Решения можно записать иначе — например в виде цилиндрических волн, разбегающихся от оси.)

Мы тогда заметили, что физически формула (21.9) относится не совсем к пустоте: в начале координат должны быть какие-то заряды, иначе расходящаяся волна не получилась бы. Иными словами, формула (21.9) есть решение уравнения (21.8) всюду, кроме непосредственной окрестности точки r=0, где (21.9) представляет собой решение полного уравнения (21.7), в правой части которого стоят источники. Давайте теперь посмотрим, что это за уравнение, т. е. какого рода источник s в уравнении (21.7) должен вызвать волну типа (21.9).

Предположим, что имеется сферическая волна (21.9) и поглядим, во что она превращается при очень малых r. Тогда запаздыванием -r/ с в f ( t - r /с) можно пренебречь, и поскольку функция f плавная, ψ превращается в

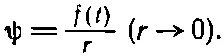(21.10)

Итак, ψ в точности похоже на кулоново поле заряда, расположенного в начале координат. Мы знаем, что для небольшого сгустка заряда, ограниченного очень малой областью близ начала координат и имеющего плотность ρ,

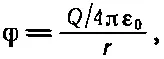
где Q=∫ρdV. Такой потенциал φ удовлетворяет уравнению

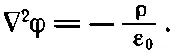
Следуя тем же расчетам, мы должны были бы сказать, что ψ из выражения (21.10) удовлетворяет уравнению

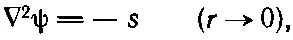(21.11)

где s связано с f формулой

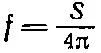
при

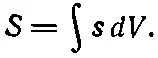
Единственная разница в том, что в общем случае s , а, стало быть, и S может оказаться функцией времени.

Далее очень важно то, что если ψ удовлетворяет (21.11) при малых r, то оно удовлетворяет также и (21.7). По мере приближения к началу координат зависимость ψ от r типа 1/r приводит к тому, что пространственные производные становятся очень большими. А производные по времени остаются теми же. [Это просто производные f ( t ) по времени.] Так что, когда r стремится к нулю, множителем ∂ 2ψ/∂ t 2в уравнении (21.7) по сравнению с ∇ 2ψ можно пренебречь, и (21.7) становится эквивалентным уравнению (21.11).

Подытоживая, можно сказать, что если функция источника s ( t ) из уравнения (21.7) сосредоточена в начале координат и ее общая величина равна

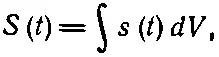(21.12)

то решение уравнения (21.7) имеет вид

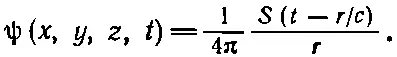(21.13)

Влияние слагаемого с ∂ 2ψ/∂ t 2в (21.7) сказывается лишь на появлении запаздывания ( t - r / с ) в потенциале кулонова типа.

Мы нашли решение уравнения (21.7) для «точечного» источника. Теперь встает новый вопрос: Каков вид решения для рассредоточенного источника? Ну, это решить легко; всякий источник s ( x, у, z, t ) можно считать состоящим из суммы многих «точечных» источников, расположенных поодиночке в каждом элементе объема dV и имеющих силу s ( x, у, z, t ) dV . Поскольку (21.7) линейно, суммарное поле представляет собой суперпозицию полей от всех таких элементов источника.

Используя результаты предыдущего параграфа [см. (21.13)], мы получим, что в момент t поле dψ в точке ( х 1, y 1,z 1) [или, короче, в точке (1)], создаваемое элементом источника sdV в точке ( х 2, у 2, z 2) [или, короче, в точке (2)], выражается формулой

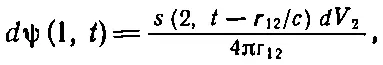
где r 12— расстояние от (2) до (1). Сложение вкладов от всех частей источника означает, конечно, интегрирование по всей области, где s≠0, так что мы имеем

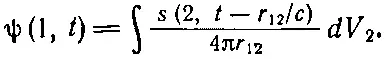(21.14)

Иначе говоря, поле в точке (1) в момент времени t представляет собой сумму всех сферических волн, испускаемых в момент t - r 12/c всеми элементами источника, расположенного в точке (2). Выражение (21.14) является решением нашего волнового уравнения для любой системы источников.