Ричард Фейнман - Том 2. Электромагнетизм и материя

Мы узнали, что ток в меняющемся диполе создает векторный потенциал в форме сферических волн, источник которых обладает силой . р/4πε 0с 2.

Теперь из B= ∇× Aможно получить магнитное поле. Поскольку . рнаправлен по оси z , у А есть только z -компонента; в роторе остаются только две ненулевые производные. Значит, В х =∂ A z /∂ y и В =—∂ A z /∂ x . Поглядим сперва на В х :

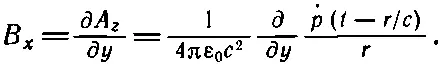(21.19)

Чтобы продифференцировать, вспомним, что r=√(x 2+y 2+z 2), так что

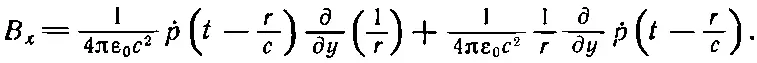(21.20)

Но мы помним, что ∂ r /∂ y = y / r ; значит, первое слагаемое даст

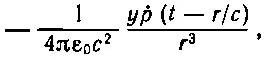(21.21)

что убывает как 1/r 2, т. е. как поле статического диполя (потому что в данном направлении у / r постоянно).

Второе слагаемое в (21.20) приводит к новому эффекту. Если провести в нем дифференцирование, то получится

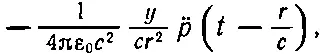(21.22)

где р " — просто вторая производная р по t . Вот это-то получающееся от дифференцирования числителя слагаемое и ответственно за излучение. Во-первых, оно описывает поле, убывающее на расстоянии как 1/ r , во-вторых, зависит от ускорения заряда. Теперь вам должно быть ясно, как мы собираемся получить формулу типа (21.1'), описывающую световое излучение.

Явление это настолько интересно и важно, что стоит немного подробнее разобраться в том, откуда берется это «радиационное» слагаемое. Мы начинали с выражения (21.18), зависящего от r как 1/ r и тем самым похожего на кулонов потенциал (если не обращать внимания на запаздывающий множитель в числителе). Почему же когда мы, желая получить поле, дифференцируем по пространственным координатам, то не получаем просто поля вида 1/r 2(конечно, с соответствующей временной задержкой)?

А вот почему. Представьте, что диполь приведен в колебательное движение вверх и вниз. Тогда

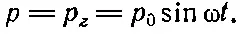
и

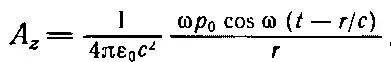
Если начертить график зависимости А r от r в каждый данный момент, то получится кривая, показанная на фиг. 21.3.

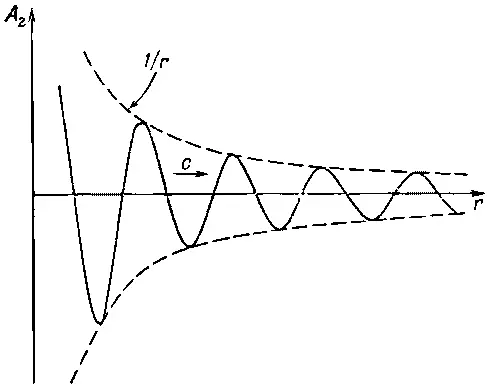
Фиг. 21.3. Зависимость величины А от r в момент t для сферической волны от колеблющегося диполя.

Амплитуда в пиках убывает как 1/ r , но, кроме того, еще имеются пространственные колебания, которые ограничены огибающей вида 1/ r . Пространственные производные в формуле пропорциональны наклону кривой. Из фиг. 21.3 видно, что встречаются намного более крутые наклоны, чем наклон самой кривой 1/ r . Очевидно, что при данной частоте наклоны в пиках пропорциональны амплитуде волны, меняющейся как 1/ r . Тем самым объясняется степень спадания радиационного слагаемого с расстоянием.

Все это получается оттого, что временные вариации в источнике превращаются в пространственные вариации, когда волны начинают разбегаться в стороны, магнитные же поля зависят от пространственных производных потенциала.

Теперь возвратимся назад и закончим наши расчеты магнитного поля. Для В х мы получили (21.21) и (21.22). Поэтому

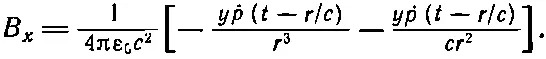(21.1')

С помощью точно таких же выкладок мы придем к

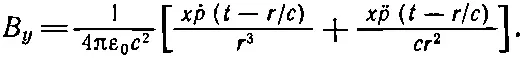
И все это можно объединить в одну красивую векторную формулу:

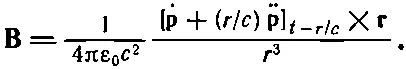(21.23)

А теперь взгляните на нее. Прежде всего на больших удалениях (когда r велико) следует принимать в расчет только .. р. Направление В дается вектором .. p×r,перпендикулярным и к радиусу r, и к ускорению (фиг. 21.4).

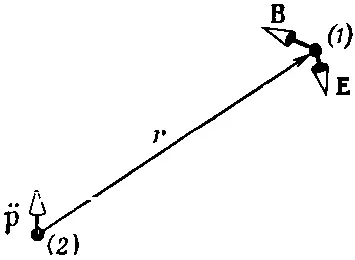
Фиг. 21.4. Поля излучения Ви Еколеблющегося диполя.

Все сходится с тем, что получилось бы из формулы (21.1').

Теперь посмотрите (к этому мы не привыкли) на то, что происходит поблизости от заряда. В гл. 14, § 7 (вып. 5) мы вывели закон Био и Савара для магнитного поля элемента тока. Мы нашли, что элемент тока j dV привносит в магнитное поле следующий вклад:

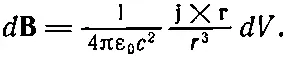(21.24)

Вы видите, что эта формула с виду очень похожа на первое слагаемое в (21.23), если только вспомнить, что . р— это ток. Но разница все же есть. В (21.23) ток надо подсчитывать в момент ( t - r / с ), а в (21.24) этого нет. На самом деле, однако, (21.24) для малых r все еще годится, потому что второе слагаемое в (21.23) стремится уничтожить эффект запаздывания из первого слагаемого. Вместе оба они приводят при малых r к результату, очень близкому к (21.24).

В этом можно убедиться следующим образом. Когда r мало, ( t - r / с ) не очень отличается от t , и в (21.23) скобки можно разложить в ряд Тэйлора. Первый член разложения дает

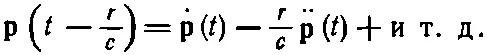
n в том же порядке по r/ с

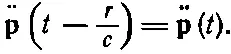
Если их сложить, члены с .. руничтожатся и слева останется незапаздывающий ток . р, т. е. . р(t) плюс члены порядка (r/с) 2и выше [например, 1/ 2(r/с) 2 ... p]. Эти члены при достаточно малых r (малых настолько, что за время r/ с ток . рзаметно не меняется) будут очень малы.

Стало быть, (21.23) приводит к полям, очень похожим на те, которые дает теория с мгновенным действием, гораздо более похожим на них, чем на поля теории с мгновенным действием и с задержкой; эффекты задержки первого порядка компенсируются вторым членом. Статические формулы очень точны, намного более точны, чем вам могло бы показаться. Конечно, компенсация чувствуется только вблизи от заряда. Для далеких точек эти поправки уже ничего не спасают, потому что временное запаздывание приводит к очень большим эффектам и в конечном счете к важному члену 1/ r — к эффекту излучения.