Ричард Фейнман - Том 2. Электромагнетизм и материя

Разумеется, угол 45° ничем не выделен. То, что индуцированная поляризация не направлена по электрическому полю, справедливо и в общем случае . Перед этим нам просто «посчастливилось» выбрать такие оси х и у , для которых поляризация Рбыла направлена по полю Е. Если бы кристалл был повернут по отношению к осям координат, то электрическое поле Е 2, направленное по оси y, вызвало бы поляризацию как по оси у , так и по оси х . Подобным же образом поляризация Р, вызванная полем, направленным вдоль оси х , тоже имела бы как х -, так и y-компоненты. Так что вместо фиг. 31.1, а мы получили бы нечто похожее на фиг. 31.1,б. Но несмотря на все это усложнение, величина поляризации Рдля любого поля Епо-прежнему пропорциональна его величине.

Рассмотрим теперь общий случай произвольной ориентации кристалла по отношению к осям координат. Электрическое поле, направленное по оси х , дает поляризацию Рс компонентами по всем трем осям, поэтому мы можем написать

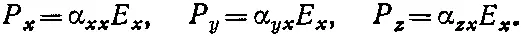(31.1)

Этим я хочу сказать лишь, что электрическое поле, направленное по оси х , создает поляризацию не только в этом направлении, оно приводит к трем компонентам поляризации Р х , Р y и P z , каждая из которых пропорциональна Е х . Коэффициенты пропорциональности мы назвали α хх , α ух и α zx(первый значок говорит, о какой компоненте идет речь, а второй относится к направлению электрического поля).

Аналогично, для поля, направленного по оси у , мы можем написать

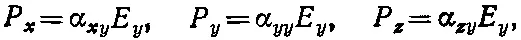(31.2)

а для поля в z-направлении

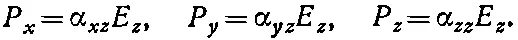(31.3)

Дальше мы говорим, что поляризация линейно зависит от поля; поэтому если у нас есть электрическое поле Ес компонентами х и у , то x-компонента поляризации Рбудет суммой двух Р х , определенных уравнениями (31.1) и (31.2), ну а если Еимеет составляющие по всем трем направлениям х, у и z, то составляющие поляризации Рдолжны быть суммой соответствующих слагаемых в уравнениях (31.1), (31.2) и (31.3). Другими словами, Рзаписывается в виде

(31.4)

Диэлектрические свойства кристалла, таким образом, полностью описываются девятью величинами (α xx ,α xy ,α xz ,α yz ,...), которые можно записать в виде символа α ij. (Индексы i и j заменяют одну из трех букв: х, у или z.) Произвольное электрическое поле Еможно разложить на составляющие Е x , Е y и Е z . Зная их, можно воспользоваться коэффициентами α ij и найти Р х , Р y и P z , которые в совокупности дают полную поляризацию Р. Набор девяти коэффициентов a ij называется тензором — в данном примере тензором поляризуемости [40] Обычно для коэффициентов пропорциональности между P и E пользуются термином тензор восприимчивости , оставляя термин поляризуемость для величин, относящихся к одной частице. Прим. ред. . Точно так же как три величины ( Е х , Е у , Е z ) «образуют вектор Е», и мы говорим, что девять величин (α хх , α ху ,...) «образуют тензор α ij».

Вы знаете, что при замене старых осей координат новыми х ', у ' и z' компоненты вектора Е х ', Е у ', Е z 'тоже оказываются другими. То же самое происходит и с компонентами Р, так что для разных систем координат коэффициенты α ij оказываются различными. Однако вполне можно выяснить, как должны изменяться а при надлежащем изменении компонент Еи Р, ибо, если мы описываем то же самое электрическое поле, но в новой системе координат, мы должны получить ту же самую поляризацию Р. Для любой новой системы координат P x'будет линейной комбинацией Р х , Р y ', и Р z':

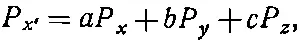
и аналогично для других компонент. Если вместо Р х , Р y и Р z подставить их выражения через Е согласно (31.4), то получится

Теперь напишите, как выражается Е х , Е y и E z через Е x ', Е y 'и Е z ', например,

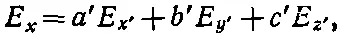
где числа а ', b ' и с ' связаны с числами а, b и c , но не равны им. Таким образом, у вас получилось выражение Р х 'через компоненты Е х ', Е y 'и E z ', т. е. получились новые α ij. Никаких хитростей здесь нет, хотя все это достаточно запутано.

Когда мы говорили о преобразовании осей, то считали, что положение самого кристалла фиксировано в пространстве . Если же вместе с осями поворачивать и кристалл, то α не изменяются. И обратно, если по отношению к осям изменять ориентацию кристалла, то получится новый набор коэффициентов а. Но если они известны для какой - то одной ориентации кристалла, то с помощью только что описанного преобразования их можно найти и для любой другой ориентации. Иначе говоря, диэлектрические свойства кристалла полностью описываются заданием компонент тензора поляризуемости α ij. в любой произвольно выбранной системе координат. Точно так же как вектор скорости v=(v x, v y , v z ) можно связать с частицей, зная, что три его компоненты при замене осей координат будут изменяться некоторым определенным образом, тензор поляризуемости α ij, девять компонент которого при изменении системы осей координат преобразуются вполне определенным образом, можно связать с кристаллом.

Связь между Ри Ев уравнении (31.4) можно записать в более компактном виде:

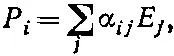(31.5)