Ричард Фейнман - Том 2. Электромагнетизм и материя

где под значком i понимается какая-то из трех букв х, у или z, а суммирование ведется по j= x, у и z. Для работы с тензорами было придумано много специальных обозначений, но каждое из них удобно для ограниченного класса проблем. Одно из таких общих соглашений состоит в том, что можно не писать знака суммы (∑) в уравнении (31.5), понимая при этом, что когда один и тот же индекс встречается дважды (в нашем случае j), то нужно просуммировать по всем значениям этого индекса. Однако, поскольку работать с тензорами нам придется немного, давайте не будем осложнять себе жизнь введением каких-то специальных обозначений или соглашений.

Потренируемся теперь в обращении с тензорами. Рассмотрим такой интересный вопрос: какая энергия требуется для поляризации кристалла (в дополнение к энергии электрического поля, которая, как известно, равна ε 0 Е 2/2 на единицу объема)? Представьте на минуту атомные заряды, которые должны быть перемещены. Работа, требуемая для перемещения одного такого заряда на расстояние dx , равна qE x dx , а если таких зарядов в единице объема содержится N штук, то для перемещения их требуется работа qE x Ndx . Но qNdx равно изменению дипольного момента единицы объема dP x . Так что работа, затраченная на единицу объема , равна

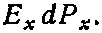
Складывая теперь работы всех трех компонент, найдем, какой должна быть работа в единице объема:

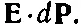
Но поскольку величина Рпропорциональна Е, то работа, затраченная на поляризацию единицы объема от 0 до Р, равна интегралу от E· d P. Обозначая ее через u P , можно написать [41] Эту работу, затраченную на создание поляризации электрическим полем, не нужно путать с потенциальной энергией —p 0 *Е постоянного дипольного момента p 0 в поле Е.

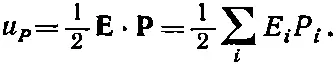(31.6)

Теперь можно воспользоваться уравнением (31.5) и выразить Рчерез E.В результате получим

(31.7)

Плотность энергии и р — величина, не зависящая от выбора осей, т. е. скаляр. Таким образом, тензор обладает тем свойством, что, будучи просуммирован по одному индексу (с вектором), он дает новый вектор, а будучи просуммирован по обоим индексам (с двумя векторами), дает скаляр.

Тензор α ijна самом деле нужно называть «тензором второго ранга», ибо у него два индекса. В этом смысле вектор, у которого всего один индекс, можно назвать «тензором первого ранга», а скаляр, у которого вообще нет индексов, — «тензором нулевого ранга». Итак, выходит, что электрическое поле Ебудет тензором первого ранга, а плотность энергии u p — тензором нулевого ранга. Эту идею можно распространить на тензоры с тремя и более индексами и определить тензоры, ранг которых выше двух.

Индексы нашего тензора поляризуемости могут принимать три различных значения, т. е. это трехмерный тензор. Математики рассматривают также тензоры размерности четыре, пять и больше. Кстати, четырехмерный тензор нам уже встречался при релятивистском описании электромагнитного поля (см. гл. 26, вып. 6) — это F μ v .

Тензор поляризуемости α ij обладает одним интересным свойством: он симметричен , т. е. α xy=α yxи т. п. для любой пары индексов. (Это свойство отражает физические качества реального кристалла, и вовсе не обязательно у любого тензора.) Вы можете самостоятельно доказать это, подсчитав изменения энергии кристалла по следующей схеме:

1) включите электрическое поле в направления оси х ;

2) включите поле в направлении оси у ;

3) выключите x -поле;

4) выключите y-поле.

Теперь кристалл вернулся к прежнему положению и полная работа, затраченная на поляризацию, должна быть нулем. Но для этого, как вы можете убедиться, α xyдолжно быть равно α yx. Однако те же рассуждения можно провести и для α xz и т. д. Таким образом, тензор поляризуемости симметричен.

Это означает также, что тензор поляризуемости можно найти простым измерением энергии, необходимой для поляризации кристалла в различных направлениях. Предположим, мы сначала взяли электрическое поле Ес компонентами х и у ; тогда, согласно уравнению (31.7),

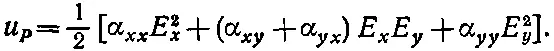(31.8)

Если бы у нас была только одна компонента Е х , мы могли бы определить α хх , а с одной компонентой Е y можно определить α yy. Включив обе компоненты Е х и Е y , мы из-за присутствия члена (α ху +α ух ) получим добавочную энергию, ну а поскольку α xyи α yxравны, то этот член превращается в 2α xyи может быть вычислен из добавочной энергии.

Выражение для энергии (31.8) имеет очень красивую геометрическую интерпретацию. Предположим, что нас интересует, какие поля Е х и Е y отвечают данной плотности энергии, скажем u 0. Возникает чисто математическая задача решения уравнения

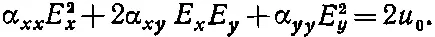
Это уравнение второй степени, так что, если мы отложим по осям величины Е х и Е y , решением этого уравнения будут все точки эллипса (фиг. 31.2).

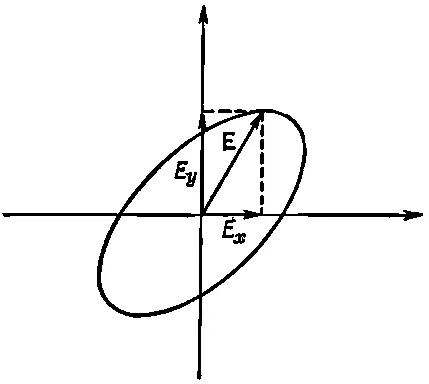
Фиг. 31.2 Конец любого вектора E=(E x , E v ), лежащего на этой кривой, дает одну и ту же анергию поляризации.

(Это должен быть именно эллипс, а не парабола и не гипербола — ведь энергия поля всегда положительна и конечна.) А само Ес компонентами Е х и Е y представляет вектор, идущий из начала координат до точки на эллипсе. Такой «энергетический эллипс» — хороший способ «увидеть» тензор поляризуемости.

Если теперь пустить в дело все три компоненты, то любой вектор Е, необходимый для создания единичной плотности энергии, задается точками, расположенными на эллипсоиде, подобно изображенному на фиг. 31.3. Форма этого эллипсоида постоянной энергии однозначно характеризует тензор поляризуемости.