Ричард Фейнман - Том 2. Электромагнетизм и материя

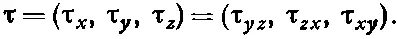
Я сказал «по случайности» потому, что это происходит только в трехмерном пространстве. Например, для четырех измерений антисимметричный тензор второго ранга имеет шесть различных ненулевых членов, и его, разумеется, нельзя заменить вектором, у которого компонент только четыре .

Точно так же как аксиальный вектор τ= r× Fявляется тензором, по тем же соображениям тензором будет и любое векторное произведение двух полярных векторов. К счастью, они тоже представимы в виде вектора (точнее, псевдовектора), что немного облегчает нам всю математику.

Вообще говоря, для любых двух векторов аи bдевять величин a i b j образуют тензор (хотя для физических целей он не всегда может быть полезен). Таким образом, для вектора положения r величины r ir jявляются тензором, а поскольку δ ij. тоже тензор, то мы видим, что правая часть (31.20) действительно является тензором. Подобным же образом тензором будет и (31.22), так как оба члена в правой части — тензоры.

Встречавшиеся до сих пор симметричные тензоры возникали как коэффициенты, связывающие один вектор с другим. Сейчас я познакомлю вас с тензором, имеющим совершенно другой физический смысл, — это тензор напряжений . Предположим, что на твердое тело действуют различные внешние силы. Мы говорим, что внутри тела возникают различные «напряжения», имея при этом в виду внутренние силы между смежными частями материала. Мы уже говорили немного о подобных напряжениях в двумерном случае, когда рассматривали поверхностное натяжение напряженной диафрагмы (см. гл. 12, § 3, вып. 5). А теперь вы увидите, что внутренние силы в материале трехмерного тела записываются в виде тензора.

Рассмотрим тело из какого-то упругого материала, например брусок из желе. Если мы разрежем этот брусок, то материал на каждой стороне разреза будет, вообще говоря, претерпевать перемещение под действием внутренних сил. До того как был сделан разрез, между двумя этими частями должны были действовать силы, которые удерживали обе части в едином куске; мы можем выразить напряжение через эти силы. Представьте себе, что мы смотрим на воображаемую плоскость, перпендикулярную оси х , подобную плоскости σ на фиг. 31.5, и интересуемся силами, действующими на маленькой площадке ΔyΔz, расположенной в этой плоскости.

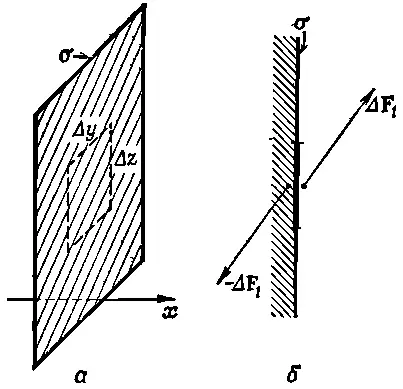
Фиг. 31.5. Материал, находящийся слева от плоскости σ на площади ΔyΔz, действует на материал, находящийся справа, с силой Δ F 1 .

Материал, находящийся слева от площадки, действует на материал с правой стороны с силой Δ F 1(фиг. 31.5, б ). Есть, конечно, и обратная реакция, т.е. на материал слева от поверхности действует сила —Δ F 1. Если площадка достаточно мала, то мы ожидаем, что сила Δ F 1пропорциональна площади ΔyΔz.

Вы уже знакомы с одним видом напряжений — статическим давлением жидкости. Там сила была равна давлению, умноженному на площадь, и направлена под прямым углом к элементу поверхности. Для твердого тела, а также движущейся вязкой жидкости сила не обязательно перпендикулярна поверхности: помимо давления (положительного или отрицательного), появляется еще и сдвигающая сила. (Под «сдвигающей» силой мы подразумеваем тангенциальные компоненты сил, действующих на поверхности.) Для этого нужно учитывать все три компоненты силы. Заметьте еще, что если разрез мы сделаем по плоскости с какой-то другой ориентацией, то действующие на ней силы тоже будут другими. Полное описание внутренних напряжений требует применения тензоров.

Определим тензор напряжений следующим образом. Вообразите сначала разрез, перпендикулярный оси х , и разложите силу Δ F 1, действующую на разрезе, на ее компоненты: Δ F x1, Δ F y1, Δ F z1(фиг. 31.6).

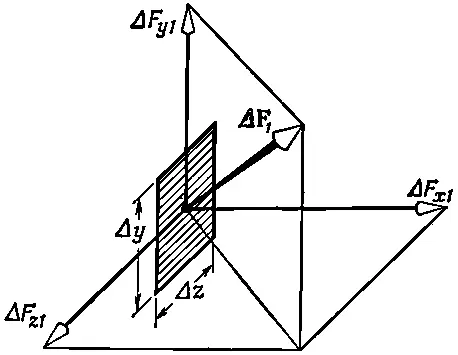
Фиг. 31.6. Сила ΔF 1 , действующая на элементе площади ΔyΔz, перпендикулярной оси х, разлагается на три компоненты: ΔF x1 , ΔF у1 и Δf z1 .

Отношение этих сил к площади ΔyΔz мы назовем S xx , S yx и S zx . Например,

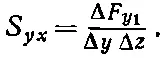
Первый индекс у относится к направлению компоненты силы, а второй х — к направлению нормали к плоскости. Если угодно, площадь ΔyΔz можно записать как Δ а х , имея в виду элемент площади, перпендикулярный оси х , т. е.

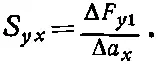
А теперь представьте себе разрез, перпендикулярный оси у . Пусть на маленькую площадку ΔxΔz действует сила Δ F 2. Разлагая снова эту силу на три компоненты, как показано на фиг. 31.7, мы определяем три компоненты напряжения S xy , S yy , S zy как силы, действующие на единичную площадь в этих трех направлениях.

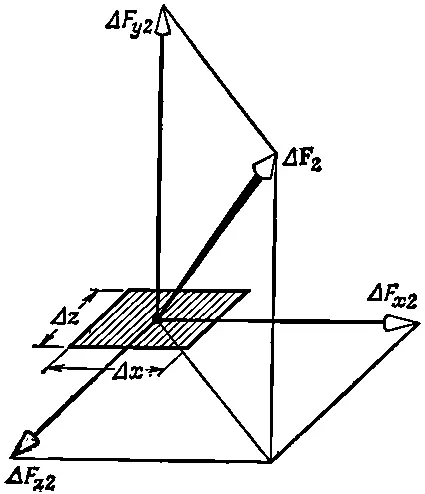
Фиг. 31.7. Сила, действующая на элемент площади, перпендикулярной оси у, разлагается на три взаимно перпендикулярные компоненты.

Наконец, проведем воображаемый разрез, перпендикулярный оси z, и определим три компоненты S xz , S yz и S zz . Таким образом, получается девять чисел:

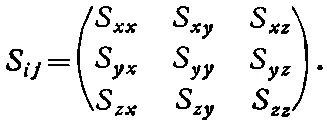(31.23)

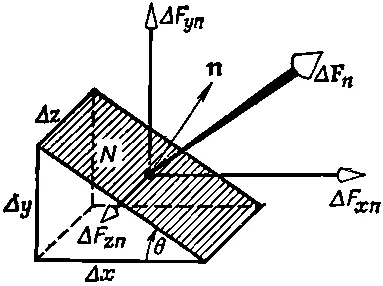
Я хочу теперь показать, что этих девяти величин достаточно, чтобы полностью описать внутреннее напряженное состояние, и что S ij —действительно тензор. Предположим, что мы хотим знать силу, действующую на поверхность, наклоненную под некоторым произвольным углом. Можно ли найти ее, исходя из S ij ? Можно, и это делается следующим образом. Вообразите маленькую призму, одна грань N которой наклонна, а другие — параллельны осям координат. Если окажется, что грань N параллельна оси z , то получается картина, изображенная на фиг. 31.8.