Ричард Фейнман - Том 2. Электромагнетизм и материя

Тензор напряжений S ij описывает внутренние силы в веществе. Если при этом материал упругий, то внутренние деформации удобно описывать с помощью другого тензора T ij— так называемого тензора деформаций . Для простого объекта, подобного бруску из металла, изменение длины ΔL, как вы знаете, приблизительно пропорционально силе, т. е. он подчиняется закону Гука

Для произвольных деформаций упругого твердого тела тензор деформаций T ij связан с тензором напряжений S ij системой линейных уравнений

(31.26)

Вы знаете также, что потенциальная энергия пружины (или бруска) равна

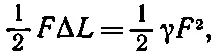
а обобщением плотности упругой энергии для твердого тела будет выражение

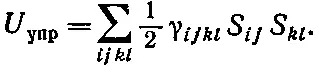(31.27)

Полное описание упругих свойств кристалла должно задаваться коэффициентами γ ijkl. Это знакомит нас с новым зверем — тензором четвертого ранга. Поскольку каждый из индексов может принимать одно из трех значений — х, у или z, то всего оказывается 3 4=81 коэффициент. Но различны из них на самом деле только 21. Во-первых, поскольку тензор S ijсимметричен, у него остается только шесть различных величин, и поэтому в уравнении (31.27) нужны только 36 различных коэффициентов. Затем, не изменяя энергии, мы можем переставить S ij и S kl , так что γ ijklдолжно быть симметрично при перестановке пары индексов ij и kl . Это уменьшает число коэффициентов до 21. Итак, чтобы описать упругие свойства кристалла низшей возможной симметрии, требуется 21 упругая постоянная! Разумеется, для кристаллов с более высокой симметрией число необходимых постоянных уменьшается. Так, кубический кристалл описывается всего тремя упругими постоянными, а для изотропного вещества хватит и двух.

В справедливости последнего утверждения можно убедиться следующим образом. В случае изотропного материала компоненты γ ijkl не должны зависеть от поворота осей. Как это может быть? Ответ : они могут быть независимы, только когда выражаются через тензоры δ ij. Но существует лишь два возможных выражения, имеющих требуемую симметрию, — это δ ijδ klи δ ikδ jl+δ il+δ jk, так что γ ijklдолжно быть их линейной комбинацией. Таким образом, для изотропного материала

следовательно, чтобы описать упругие свойства материала, требуются две постоянные: а и b. Я предоставляю вам самим доказать, что для кубического кристалла требуются три такие постоянные.

И еще один последний пример (на этот раз пример тензора третьего ранга) дает нам пьезоэлектрический эффект. При напряженном состоянии в кристалле возникает электрическое поле, пропорциональное тензору напряжений. Общий закон пропорциональности имеет вид

где E i — электрическое поле, а P ijk — пьезоэлектрические коэффициенты (пьезомодули), составляющие тензор. Можете ли вы сами доказать, что если у кристалла есть центр инверсии (т. е. если он инвариантен относительно замены х, у, z →- х ,- y ,-z), то все его пьезоэлектрические коэффициенты равны нулю.

Все тензоры, с которыми мы сталкивались в этой главе, были связаны с трехмерным пространством; они определялись как величины, имеющие известные трансформационные свойства при пространственных поворотах. А вот в гл. 26 (вып. 6) мы имели возможность воспользоваться тензором в четырехмерном пространстве-времени: это был тензор электромагнитного поля F μv. Компоненты такого четырехмерного тензора особым образом преобразуются при преобразованиях Лоренца. (Мы этого, правда, не делали, но могли бы рассматривать преобразования Лоренца как своего рода «вращение» в четырехмерном «пространстве», называемом пространством Минковского; тогда аналогия с тем, что мы рассматривали здесь, была бы ярче.)

В качестве последнего примера мы хотим рассмотреть другой тензор в четырех измерениях ( t, x, y, z ) теории относительности. Когда мы говорили о тензоре напряжений, то определяли S ij как компоненту силы, действующую на единичную площадку. Но сила равна скорости изменения импульса со временем. Поэтому вместо того, чтобы говорить «S xy— это х -компонента силы, действующей на единичную площадку, перпендикулярную оси у », мы с равным правом могли бы сказать: «S xy— это скорость потока x-компоненты импульса через единичную площадку, перпендикулярную оси у ». Другими словами, каждый член S ijпредставляет поток i-й компоненты импульса через единичную площадку, перпендикулярную оси j. Так обстоит дело с чисто пространственными компонентами, но они составляют только часть «большего» тензора S μ v в четырехмерном пространстве (μ и v = t, x, у, z ), содержащего еще дополнительные компоненты S tx , S yt , S tt и т. п. Попытаемся теперь выяснить физический смысл этих дополнительных компонент.

Нам известно, что пространственные компоненты представляют поток импульса. Чтобы найти ключ к распространению этого понятия на «временное направление», обратимся к «потоку» другого рода — потоку электрического заряда. Скорость потока скалярной величины, подобной заряду (через единичную площадь, перпендикулярную потоку), является пространственным вектором — вектором плотности тока j. Мы видели, что временная компонента вектора потока — это плотность текущего вещества. Например, jможно скомбинировать с плотностью заряда j t=ρ и получить четырехвектор j μ=(ρ, j), т. е. значок μ у вектора j μпринимает четыре значения: t, х, у, z . Это означает «плотность», «скорость потока в x-направлении», «скорость потока в y-направлении» и «скорость потока в z-направлении» скалярного заряда.

Теперь по аналогии с нашим утверждением о временной компоненте потока скалярной величины можно ожидать, что вместе с S xx , S xy и S xz , описывающими поток x-компоненты импульса, должна быть и временная компонента S xt , которая по идее должна бы описывать плотность того, что течет, т. е. S xt должна быть плотностью х-компоненты импульса. Таким образом, мы можем расширить наш тензор по горизонтали, включив в него t-компоненты, и в нашем распоряжении оказываются: