Ричард Фейнман - Том 2. Электромагнетизм и материя

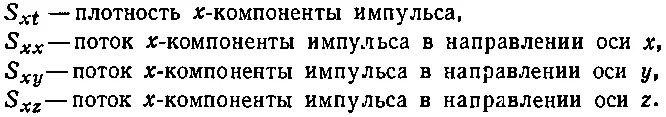
Аналогичная вещь происходит и с y-компонентой; у нас есть три компоненты потока: S yx , S yy и S yz , к которым нужно добавить четвертый член:

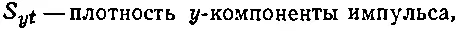
а к трем компонентам S zx , S zy и S zz мы добавляем

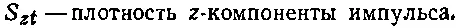
В четырехмерном пространстве у импульса существует также и t-компонента, которой, как мы знаем, является энергия. Так что тензор S ij следует продолжить по вертикали с включением в него S tx , S ty и S tz , причем

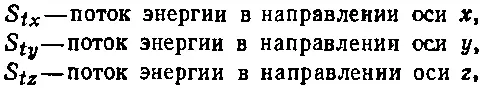(31.28)

т. е. S tx — это поток энергии в единицу времени через поверхность единичной площади, перпендикулярную оси х , и т. д. Наконец, чтобы пополнить наш тензор, нужна еще величина S tt , которая должна быть плотностью энергии . Итак, мы расширили наш трехмерный тензор напряжений до четырехмерного тензора энергии - импульса S μ v . Индекс μ может принимать четыре значения: t, х, у и z, которые означают «плотность», «поток через единичную площадь в направлении оси х », «поток через единичную площадь в направлении оси y» и «поток через единичную площадь в направлении оси z». Значок v тоже принимает четыре значения: t, х, у, z , которые говорят нам, что же именно течет: «энергия», x-компонента импульса», «y-компонента импульса» или же «z-компонента импульса».

В качестве примера рассмотрим этот тензор не в веществе, а в пустом пространстве с электромагнитным полем. Вы знаете, что поток энергии электромагнитного поля описывается вектором Пойнтинга S=ε 0c 2 E× В. Так что х -, у - и z-компоненты вектора Sс релятивистской точки зрения являются компонентами: S tx , S ty и S tz нашего тензора энергии-импульса. Симметрия тензора S ij переносится и на временные компоненты, так что четырехмерный тензор S μvтоже симметричен:

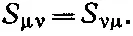(31.29)

Другими словами, компоненты S xt , S yt , S zt , которые представляют плотности х -, у - и z-компонент импульса , равны также х -, у - и z-компонентам вектора Пойнтинга S, или, как мы видели раньше из других соображений, вектора потока энергии .

Оставшиеся компоненты тензора электромагнитного напряжения S μ v тоже можно выразить через электрическое и магнитное поля Еи В. Иначе говоря, для электромагнитного поля в пустом пространстве мы должны допустить существование тензора напряжений, или, выражаясь менее таинственно, потока импульса электромагнитного поля. Мы уже обсуждали это в гл. 27 (вып. 6) в связи с уравнением (27.21), но тогда мы не входили в детали.

Тем из вас, кто хочет испытать свою удаль на четырехмерных тензорах, может понравиться выражение для тензора S μ v через поля:

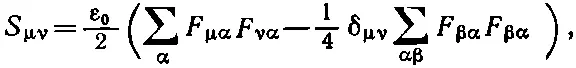
где суммирование по α и β проводится по всем их значениям (т. е. t, x, у и z ), но, как обычно в теории относительности, для суммы ∑ и символа δ принимается специальное соглашение. В суммах слагаемые со значками х, у, z должны вычитаться , а δ tt=+1, тогда как δ xx.=δ уу=δ zz=-1 и δ μv=0 для всех μ≠ v (с=1). Сможете ли вы доказать, что эта формула приводит к плотности энергии S tt =(ε 0/2)( E 2+ B 2) и вектору Пойнтинга [42] Если не полагать с=1, как это делается здесь, то плотность энергии в принятых в книге единицах будет равна (ε 0 /2)( E 2 + с 2 B 2 ) или в единицах СИ 1 / 2 [ε 0 E 2 +( l /μ 0 ) B 2 ]. — Прим. ред. ε 0 Е× В? Можете ли вы показать, что в электростатическом поле, когда В=0, главная ось напряжения направлена по электрическому полю и вдоль направления поля возникает натяжение (ε 0/2) E 2и равное ему давление в направлении, перпендикулярном направлению поля?

Повторить : всё что в табл. 32.

Здесь я хочу обсудить явления преломления света, ну и, разумеется, его поглощение плотным веществом. Теорию показателя преломления мы уже рассматривали в гл. 31 (вып. 3), но тогда наши знания математики были весьма ограничены и мы остановились только на показателе преломления веществ с малой плотностью наподобие газов. Но физические принципы, приводящие к возникновению показателя преломления, мы там все же выяснили. Электрическое поле световой волны поляризует молекулы газа, создавая тем самым осциллирующие дипольные моменты, а ускорение осциллирующих зарядов приводит к излучению новых волн поля. Это новое поле, интерферируя со старым, изменяет его. Изменение поля эквивалентно тому, что происходит сдвиг фазы первоначальной волны. Из-за того что сдвиг фазы пропорционален толщине материала, эффект в целом оказывается эквивалентным изменению фазовой скорости света в материале. Прежде, когда рассматривалось это явление, мы пренебрегали усложнениями, возникающими от таких эффектов, как действие новой измененной волны на поле осциллирующего диполя. Мы предполагали, что силы, действующие на заряды атомов, определяются только падающей волной, тогда как на самом деле на осциллятор действует не только падающая волна, но и волны, излученные другими атомами. В то время нам еще было трудно учесть этот эффект, поэтому мы изучали только разреженные газы, где его можно считать несущественным.

Ну а теперь мы увидим, что эта задача с помощью дифференциальных уравнений решается совсем просто. Конечно, дифференциальные уравнения затуманивают физическую причину возникновения преломления (как результата интерференции вновь излученных волн с первоначальными), но зато они упрощают теорию плотного материала. В этой главе сойдется вместе многое из того, что мы делали уже раньше. Практически мы уже получили все, что нам потребуется, так что по-настоящему новых идей в этой главе будет сравнительно немного. Поскольку вам может понадобиться освежить в памяти то, с чем мы здесь столкнемся, то в табл. 32.1 приводится список уравнений, которые я собираюсь использовать вместе со ссылкой на те места, где их можно найти. Во многих случаях из-за нехватки времени я не смогу снова останавливаться на физических аргументах, а сразу же буду браться за уравнения.