Ричард Фейнман - Том 2. Электромагнетизм и материя

Таблица 32.1. ЧТО БУДЕТ ИСПОЛЬЗОВАНО В ЭТОЙ ГЛАВЕ

Начну с напоминания о механизме преломления в газе. Мы предполагаем, что в единице объема газа находится N частиц и каждая из них ведет себя как гармонический осциллятор. Мы пользуемся моделью атома или молекулы, к которой электрон привязан силой, пропорциональной его перемещению (как будто он удерживается пружинкой). Отметим, что такая модель атома с классической точки зрения незаконна, однако позднее будет показано, что правильная квантовомеханическая теория дает (в простейших случаях) эквивалентный результат. В наших прежних рассмотрениях мы не учитывали «тормозящей» силы в атомном осцилляторе, а сейчас это будет сделано. Такая сила соответствует сопротивлению при движении, т. е. она пропорциональна скорости электрона. Уравнением движения при этом будет

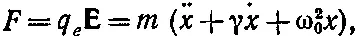(32.1)

где х — перемещение, параллельное направлению поля Е. (Осциллятор предполагается изотропным , т. е. восстанавливающая сила одинакова во всех направлениях. Кроме того, на время мы ограничимся линейно поляризованной волной, так что поле Ене меняет своего направления.) Если действующее на атом электрическое поле изменяется со временем синусоидально, то мы пишем.

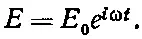(32.2)

С той же самой частотой будет осциллировать и перемещение, поэтому можно считать

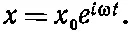
Подставляя . х = i ω х и .. х =-ω 2х, можно выразить х через Е :

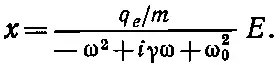(32.3)

А зная перемещение, можно вычислить ускорение .. х и найти ответственную за преломление излученную волну. Именно таким способом в гл. 31 (вып. 3) мы подсчитывали показатель преломления.

Теперь же мы пойдем другим путем. Индуцированный дипольный момент атома р равен q e x , или в силу уравнения (32.3)

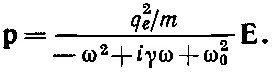(32.4)

Так как рпропорционально Е, то мы пишем

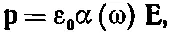(32.5)

где α — атомная поляризуемость [43] Всюду в этой главе мы будем пользоваться обозначениями, принятыми в гл. 31 (вып. 3); пусть α — атомная поляризуемость, как это определено здесь. В предыдущей главе мы пользовались буквой α для обозначения объемной поляризуемости, т. е. отношения Р к Е. Но в обозначениях этой главы P=Nαε 0 E [см. выражение (32.8)]. :

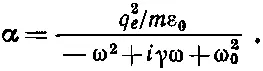(32.6)

Подобный же ответ для движения электронов в атоме дает и квантовая механика, но с учетом следующих особенностей. У атомов есть несколько собственных частот, каждая из которых имеет свою диссипативную постоянную γ. Кроме того, каждая гармоника имеет еще свою эффективную «силу», выражаемую в виде произведения поляризуемости при данной частоте на постоянную связи f , которая, как ожидается, по порядку величины равна единице. Обозначая каждый из трех параметров ω 0, γ и f для каждой из гармоник через ω 0k, γ kи f kи суммируя по всем гармоникам, мы вместо (32.6) получаем

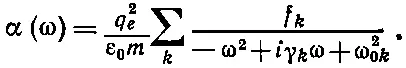(32.7)

Если число атомов в единице объема вещества равно N , то поляризация Рбудет просто Np =ε 0 N α E , т. е. пропорциональна Е :

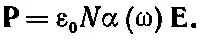(32.8)

Другими словами, когда на материал действует синусоидальное электрическое поле, оно индуцирует пропорциональный себе дипольный момент, причем константа пропорциональности α, как мы уже отмечали, зависит от частоты. При очень больших частотах α мала: реакция материала слабая. А вот при низких частотах реакция может быть очень сильной. Константа пропорциональности, кроме того, еще оказывается комплексной, т. е. поляризация не следует точно за всеми изменениями электрического поля, а в какой-то степени может быть сдвинута по фазе. Во всяком случае, электрическое поле вызывает в материале поляризацию, пропорциональную его напряженности.

Наличие в веществе поляризации означает, что там возникают поляризационные заряды и токи, которые необходимо учитывать в полных уравнениях Максвелла при нахождении полей. Сейчас мы собираемся решать уравнения Максвелла для случая, когда заряды и токи не равны нулю, но неявно определяются вектором поляризации. Нашим первым шагом должно быть явное нахождение плотности зарядов ρ и плотности тока j,усредненных по тому же самому малому объему, который имелся в виду при определении вектора Р. Потом необходимые нам значения ρ и j могут быть определены из поляризации. В гл. 10 (вып. 5) мы видели, что когда поляризация Рменяется от точки к точке, то возникает плотность зарядов:

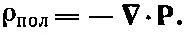(32.9)

В то время мы имели дело со статическими полями, но эта же формула справедлива и для переменных полей. Но когда Ризменяется со временем, заряды движутся, так что появляется поляризационный ток . Каждый из осциллирующих зарядов вносит в ток свой вклад, равный произведению его заряда q e на скорость v . Когда же таких зарядов в единице объема N штук, то они создают плотность тока j:

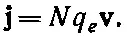
Ну а поскольку известно, что v = dx / dt , то j = Nq e dx / dt , что как раз равно dP/dt. Следовательно, при переменной поляризации возникает плотность тока

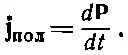(32.10)