Ричард Фейнман - Том 2. Электромагнетизм и материя

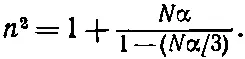(32.31)

Более удобно переписать это в виде

(32.32)

который алгебраически эквивалентен прежнему. Это и есть известная формула Клаузиуса — Моссотти.

В плотном материале возникает и другое усложнение. Поскольку атомы расположены слишком тесно, они сильно взаимодействуют друг с другом. Поэтому внутренние гармоники осцилляции изменяются. Собственные частоты атомных осцилляций размазываются этими взаимодействиями и обычно весьма сильно подавляются ими, а коэффициент трения становится очень большим. Таким образом, все ω 0и γ твердого вещества будут другими, чем для свободных атомов. С этой оговоркой мы все-таки можем представлять α, по крайней мере приближенно, уравнением (32.7), так что

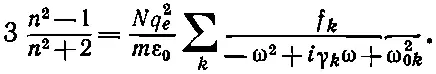(32.33)

Наконец, последнее усложнение. Если плотный материал представляет собой смесь нескольких компонент, то каждая из них дает свой вклад в поляризацию. Полная α будет суммой вкладов различных компонент смеси [за исключением неточности приближения локального поля в упорядоченных кристаллах, т. е. выражения (32.28) — эффекты, которые мы обсуждали при разборе сегнетоэлектриков]. Обозначая через N j число атомов каждой компоненты в единице объема, мы должны заменить формулу (32.32) следующей:

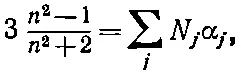(32.34)

где каждая α jбудет определяться выражением типа (32.7). Выражение (32.34) завершает нашу теорию показателя преломления. Величина 3(n 2-1)/(n 2+2) задается комплексной функцией частоты, каковой является средняя атомная поляризуемость α(ω). Точное вычисление α(ω) (т. е. нахождение f k , γ k и ω 0k) для плотного вещества — одна из труднейших задач квантовой механики. Это было сделано только для нескольких особенно простых веществ.

Обсудим теперь следствия нашего результата (32.33). Прежде всего обратите внимание на то, что α — комплексное число, так что показатель преломления n тоже оказывается комплексным. Что это означает? Давайте возьмем и запишем n в виде вещественной и мнимой частей:

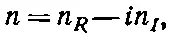(32.35)

где n R и n I — вещественные функции ω. Мы написали in I с отрицательным знаком, так что n I для обычных оптических материалов будет положительной величиной. (Для обычных оптически неактивных материалов, которые не служат сами источниками света, как это происходит у лазеров, γ—положительное число, а это делает мнимую часть n отрицательной.) Наша плоская волна запишется теперь через n следующим образом:

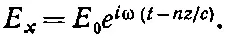
Если подставить n в виде выражения (32.35), то мы получим

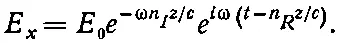(32.36)

Множитель exp [ i ω( t - n R z / c )] представляет просто волну, бегущую со скоростью c / n R , т. е. n R будет как раз то, что мы обычно считаем показателем преломления. Но амплитуда этой волны равна

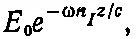
и с увеличением z она экспоненциально убывает. График напряженности электрического поля как функции от z в некоторый момент времени и для n I≈ n R /2π показан на фиг. 32.1.

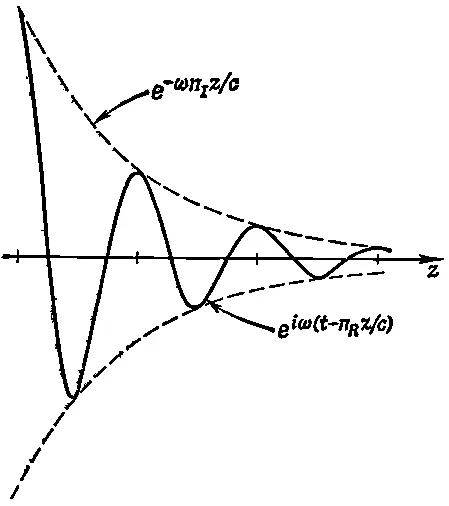
Фиг. 32.1. График поля Е х в некоторый момент t при n I ≈n R 2/π.

Мнимая часть показателя преломления из-за потерь энергии в атомных осцилляторах приводит к ослаблению волны. Интенсивность волны пропорциональна квадрату амплитуды, так что

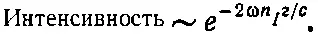
Часто это записывается как

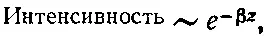
где β=2ωn I/с — коэффициент поглощения . Таким образом, в уравнении (32.33) содержится не только теория показателя преломления вещества, но и теория поглощения им света.

В тех материалах, которые мы обычно считаем прозрачными, величина c/ωn I, имеющая размерность длины, оказывается гораздо больше толщины материала.

В нашей теории показателя преломления имеется еще одно предсказание, которое можно проверить экспериментально. Предположим, что мы рассматриваем смесь двух материалов. Показатель преломления смеси не будет средним двух показателей, а определяется через сумму двух поляризуемостей, как в уравнении (32.34). Если, скажем, мы интересуемся показателем преломления раствора сахара, то полная поляризуемость будет суммой поляризуемостей воды и сахара. Но каждая из них, разумеется, должна подсчитываться исходя из данных о числе молекул N данного сорта в единице объема. Другими словами, если в данном растворе содержится N 1молекул воды, поляризуемость которой α 1, и N 2молекул сахарозы (C 12H 22O 11), поляризуемость которой α 2, то мы должны получить

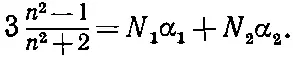(32.37)

Этой формулой можно воспользоваться для экспериментальной проверки нашей теории — измерения показателя для различных концентраций сахарозы в воде. Однако здесь мы должны сделать несколько допущений. Наша формула предполагает, что при растворении сахарозы никакой химической реакции не происходит и что возмущение индивидуальных осцилляторов при различных частотах отличается не слишком сильно. Поэтому наш результат, безусловно, будет только приближенным. Тем не менее давайте посмотрим, насколько он хорош.

Раствор сахара мы выбрали потому, что мы располагаем хорошими данными измерений показателя преломления [44] Взяты из справочника «Handbook of Physics and Chemistry». и, кроме того, сахар представляет собой молекулярный кристалл и переходит в раствор без ионизации и других изменений химического состояния.