Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Таблица 32.2.ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ РАСТВОРА САХАРА И СРАВНЕНИЕ С ПРЕДСКАЗАНИЕМ УРАВНЕНИЯ (32.37)
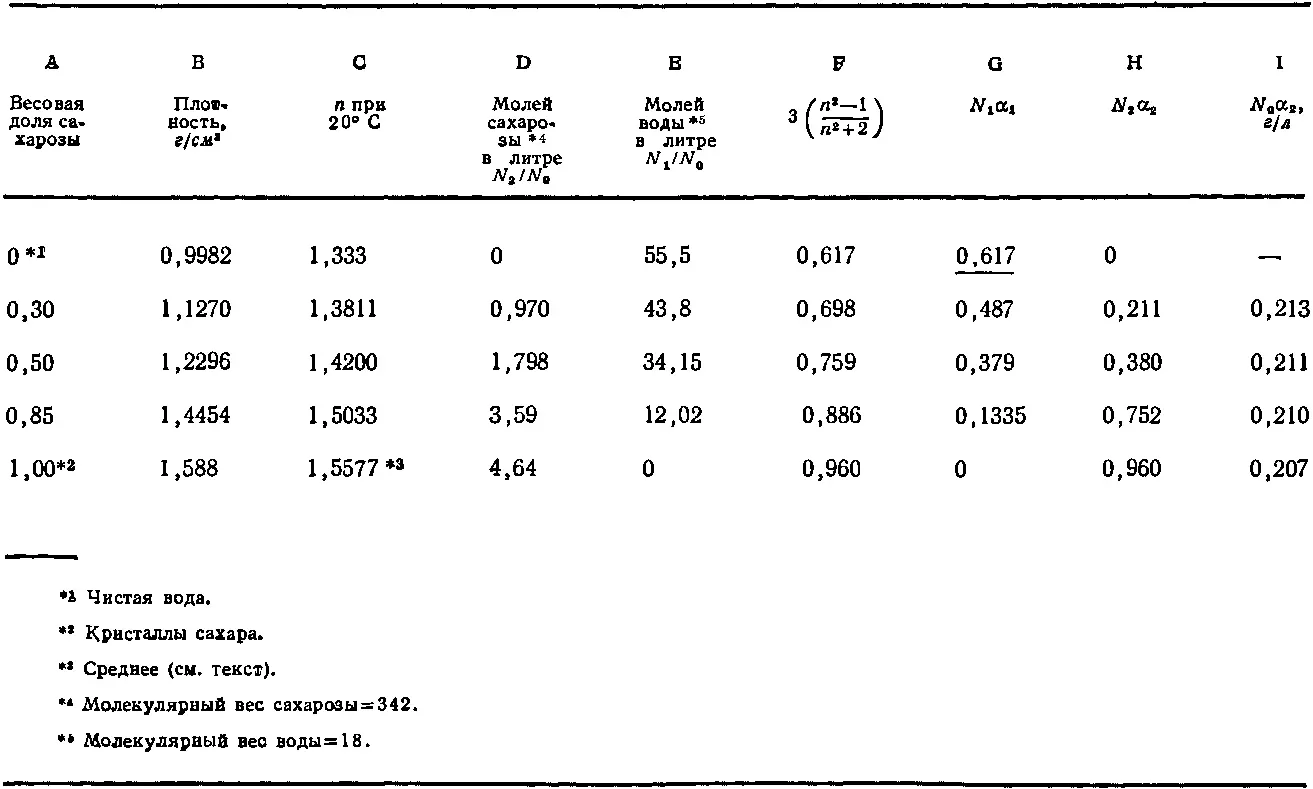
В первых трех столбцах табл. 32.2 приведены данные из указанного справочника. В столбце А дан процент сахарозы по весу, в столбце В приведена измеренная плотность в г / см 3, а в столбце С даны измерения показателя преломления света с длиной волны 589,3 ммк . В качестве показателя чистого сахара мы взяли результаты измерений для кристалла сахара. Эти кристаллы не изотропны, так что показатель преломления в разных направлениях различен. Справочник дает три величины:
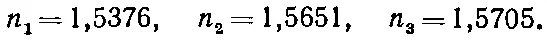
Мы взяли среднее.
Попытаемся теперь подсчитать n для каждой концентрации, но мы не знаем, какие нужно взять значения α 1и α 2. Проверим теорию таким способом: будем предполагать, что поляризуемость воды (α 1) при всех концентрациях одна и та же, и подсчитаем поляризуемость сахарозы, используя экспериментальную величину n и разрешая (32.37) относительно α 2. Если теория верна, то мы для любой концентрации должны получить одно и то же значение α 2.
Прежде всего нам нужно знать числа N 1и N 2; выразим их через число Авогадро N 0. В качестве нашей единицы объема давайте возьмем один литр (1000 см 3). Тогда отношение N i / N 0равно весу одного литра, поделенному на грамм-молекулу. А вес литра равен произведению плотности (умноженной на 1000, чтобы получить граммы) на весовую долю либо сахарозы, либо воды. Таким путем получаем N 2/ N 0и N 1/ N 0, записанные в столбцах D и Е нашей таблицы.
В столбце F мы подсчитали 3(n 2-1)/(n 2+2), исходя из экспериментальных значений n (столбец С). Для чистой воды 3(n 2-1)/(n 2+2) равно 0,617, что как раз будет N 1α 1. Затем мы можем заполнить остальную часть колонки G, поскольку для каждой строки отношение G/E должно быть одной и той же величиной, именно 0,617:55,5. Вычитая столбец G из столбца F, находим вклад N 2α 2, вносимый сахарозой, который записан в столбце Н. А затем, поделив эти данные на величину N 2/ N 0из столбца D, мы получаем величину N 0α 2, приведенную в столбце 1.
Из нашей теории мы ожидали, что все величины N 0α 2должны получиться одинаковыми. Они получились хотя и не точно равными, но довольно близкими друг к другу. Отсюда можно заключить, что наши идеи правильны. Более того, мы нашли, что поляризуемость молекул сахара, по-видимому, не зависит сильно от ее окружения: их поляризуемость приблизительно одна и та же как в разбавленном растворе, так и в кристалле.
§ 6. Волны в металлах
Теорию, которая в этой главе развивалась для твердых материалов, после очень небольшой модификации вполне можно применить и к хорошим проводникам типа металлов. На некоторые из электронов в металлах не действует сила, привязывающая их к какому-то частному атому; это так называемые «свободные» электроны, ответственные за проводимость. Там есть и другие электроны, которые связаны в атомах, и изложенная выше теория непосредственно приложима именно к ним. Однако их влияние обычно «забивается» эффектами электронов проводимости. Поэтому сейчас мы рассмотрим только эффекты свободных электронов.
Если на электрон не действует никакая восстанавливающая сила, но сопротивление его движению все же остается, то уравнение движения электрона отличается от (32.1) только отсутствием члена ω 0 2 х . Так что единственное, что нам нужно сделать, — это положить ω 0 2=0 во всей остальной части наших выводов. Но есть еще одно отличие. В диэлектриках мы должны различать среднее и локальное поля и вот почему: в изоляторе каждый из диполей занимает фиксированное положение по отношению к другим диполям. Но в металле из-за того, что электроны проводимости движутся и меняют свое место, поле, действующее на них, в среднем как раз равно среднему полю Е. Так что поправка, которую мы сделали к формуле (32.5), не годится, т. е. применение формулы (32.28) для электронов проводимости недопустимо . Следовательно, выражение для показателя преломления в металле должно выглядеть подобно выражению (32.27), в котором следует положить ω 0=0, именно:
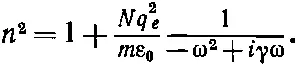 (32.38)
(32.38)
Это только вклад от электронов проводимости, которые, как мы думаем, играют в металлах главную роль.
Но теперь мы даже знаем, какой нам взять величину γ, ибо она связана с проводимостью металла. В гл. 43 (вып. 4) мы обсудили связь проводимости металлов с диффузией свободных электронов в кристалле. Электроны движутся по ломаному пути от одного соударения до другого, а между этими толчками они летят свободно, за исключением ускорения из-за какого-то среднего электрического поля (фиг. 32.2).
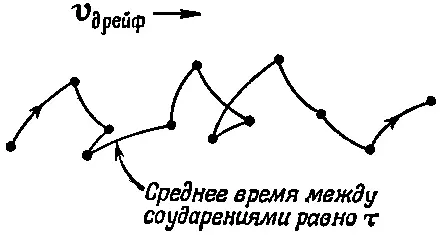
Фиг. 32.2. Движение свободного электрона.
Там же, в гл. 43 (вып. 4), мы нашли, что средняя скорость дрейфа равна просто произведению ускорения на среднее время между соударениями τ. Ускорение равно q e E / m , так что
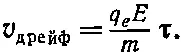 (32.39)
(32.39)
В этой формуле поле Есчитается постоянным, так что скорость v дрейфтоже постоянна. Поскольку в среднем ускорение отсутствует, сила торможения равна приложенной силе. Мы определили γ через силу торможения, равную γ mv [см. (32.1)], или q e E , поэтому получается, что
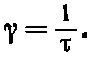 (32.40)
(32.40)
Несмотря на то что мы не можем с легкостью измерять непосредственно τ, можно определять его, измеряя проводимость металла. Экспериментально обнаружено, что электрическое поле Епорождает в металлах ток с плотностью j, пропорциональной Е(для изотропного материала, конечно):
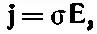
причем постоянная пропорциональности σ называется проводимостью .
В точности то же самое мы ожидаем из выражения (32.39), если положить
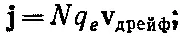
Интервал:
Закладка:






