Ричард Фейнман - Том 2. Электромагнетизм и материя

Наша задача стала теперь простой и понятной. Мы пишем уравнения Максвелла с плотностями заряда и тока, определяемыми поляризацией Рпосредством уравнений (32.9) и (32.10). (Предполагается, что других зарядов и токов в веществе нет.) Затем мы свяжем Рс Еформулой (32.5) и будем разрешать их относительно Еи В, отыскивая при этом волновое решение.

Но прежде чем приступить к решению, мне бы хотелось сделать одно замечание исторического характера. Первоначально Максвелл писал свои уравнения в форме, отличающейся от той, в которой они используются нами. И именно потому, что уравнения писались в другой форме в течение многих лет (да и сейчас многими пишутся так), я постараюсь объяснить вам разницу. В те дни механизм диэлектрической проницаемости не был понятен с ясностью и полнотой. Не была ясна ни природа атомов, ни существование поляризации в веществе. Поэтому тогда не понимали, что ∇· Pдает дополнительный вклад в плотность заряда ρ. Были известны только заряды, не связанные в атомах (такие, как заряды, текущие по проводу или возникающие при трении).

Сегодня же мы предпочитаем обозначать через ρ полную плотность зарядов, включая в нее и заряды, связанные с индивидуальными атомами. Если назвать эту часть зарядов ρ пол, то можно написать

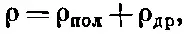
где ρ др— плотность зарядов, учтенная Максвеллом и относящаяся к другим зарядам, не связанным с определенными атомами. При этом мы бы написали

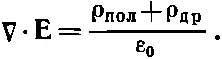
После подстановки ρ полиз (32.9) получаем

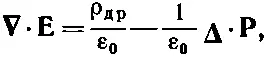
или

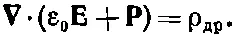(32.11)

В плотность тока, фигурирующую в уравнениях Максвелла для ∇× B, вообще говоря, тоже вносится вклад от связанных атомных электронных токов. Поэтому мы можем написать

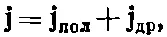
причем уравнение Максвелла приобретает вид

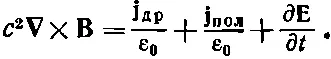(32.12)

Используя уравнение (32.10), получаем

(32.13)

Теперь вы видите, что если бы мы определили новый вектор D

(32.14)

то два уравнения поля приняли бы вид

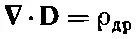(32.15)

и

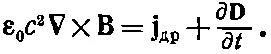(32.16)

Это и есть та форма уравнений, которую использовал Максвелл для диэлектриков. А вот и остальные два уравнения:

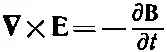
и

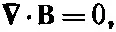
которые в точности совпадают с нашими.

Перед Максвеллом и другими учеными того времени вставала проблема магнетиков (за них мы вскоре примемся). Они ничего не знали о циркулирующих токах, ответственных за атомный магнетизм и поэтому, в плотности тока утеряли еще одну часть. Вместо уравнения (32.16) они на самом деле писали

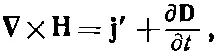(32.17)

где Нотличается от ε 0с 2 В, так как последнее учитывает эффекты атомных токов. (При этом j'представляет то, что осталось от токов.) Таким образом, у Максвелла было четыре полевых вектора: Е, D, Ви Н, причем в Dи Нскрывалось то, на что он не обратил внимания, — процессы, происходящие внутри вещества. Уравнения, написанные в таком виде, вы встретите во многих местах.

Чтобы решить их, необходимо как-то связать Dи Нс другими полями, поэтому зачастую писали

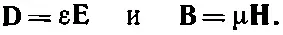(32.18)

Однако эти связи верны лишь приближенно для некоторых веществ, и то лишь когда поля не изменяются слишком быстро со временем. (Для синусоидально изменяющихся полей зачастую можно писать уравнения таким способом, считая при этом ε и μ комплексными функциями частоты, но для произвольных изменений поля со временем это неверно.) На какие только ухищрения не пускаются ученые, чтобы решить уравнения! А мне кажется, что правильнее всего оставить уравнения записанными через фундаментальные величины, как мы понимаем их теперь, т. е. как раз то, что мы и проделали.

Теперь нам предстоит выяснить, какого сорта электромагнитные волны могут существовать в диэлектрическом веществе, где других зарядов, кроме тех, что связаны в атомах, нет. Таким образом, мы возьмем ρ=-∇· Ри j=∂ P/∂t. При этом уравнения Максвелла примут такой вид:

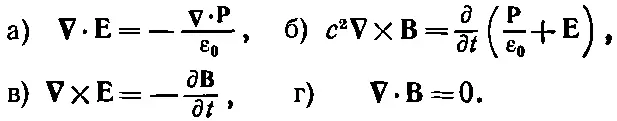(32.19)

Мы можем решить эти уравнения, как делали это прежде. Начнем с применения к уравнению (32.19в) операции ротора:

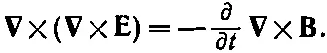
Используя затем векторное тождество

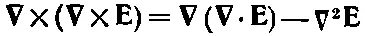
и подставляя выражение для ∇× Bиз (32.19б), получаем

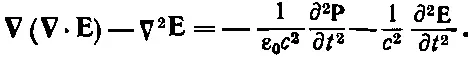
Используя уравнение (32.19а) для ∇· Е, находим

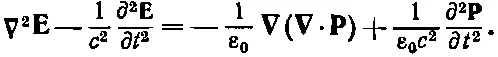(32.20)