Ричард Фейнман - Том 2. Электромагнетизм и материя

тогда

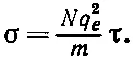(32.41)

Таким образом, τ, а следовательно, и γ могут быть связаны с наблюдаемой электрической проводимостью. Используя (32.40) и (32.41), можно переписать нашу формулу (32.38) для показателя преломления в виде

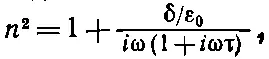(32.42)

где

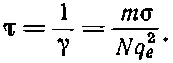(32.43)

Это и есть известная формула для показателя преломления в металлах.

Наш результат для показателя преломления в металлах —формула (32.42) — предсказывает для распространения волн с разными частотами совершенно различные характеристики. Прежде всего давайте посмотрим, что получается при низких частотах. Если величина ω достаточно мала, то (32.42) можно приближенно записать в виде

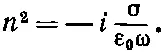(32.44)

Возведением в квадрат [45] Или записав — i=е -iπ/2 ; √-i=e -iπ/4 =соsπ/4-isinπ/4, что приводит к тому же результату. можно проверить, что

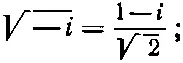
таким образом, для низких частот

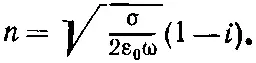(32.45)

Вещественная и мнимая части n имеют одну и ту же величину. С такой большой мнимой частью n волны в металлах затухают очень быстро. В соответствии с выражением (32.36) амплитуда волны, идущей в направлении оси z, уменьшается как

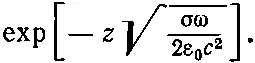(32.46)

Запишем это в виде

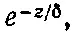(32.47)

где δ — это то расстояние, на котором амплитуда волны уменьшается в е=2,72 раза, т. е. приблизительно в 3 раза. Амплитуда такой волны, как функция от z , показана на фиг. 32.3.

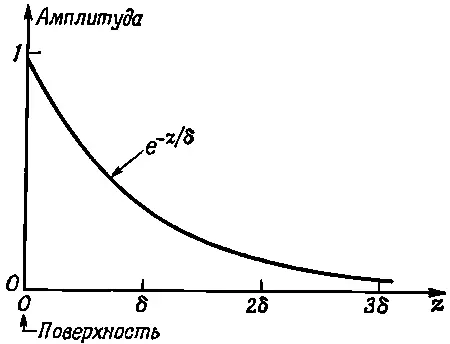
Фиг. 32.3. Амплитуда поперечной электромагнитной волны в металле как функция расстояния.

Поскольку электромагнитные волны проникают в глубь металла только на это расстояние, величина δ называется глубиной скин - слоя и определяется выражением

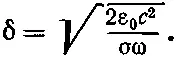(32.48)

Но что все-таки мы понимаем под «низкими» частотами? Взглянув на уравнение (32.42), мы видим, что его можно приближенно заменить уравнением (32.44), только когда ωτ много меньше единицы и когда ωε 0/σ также много меньше единицы, т. е. наше низкочастотное приближение применимо при

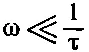
и

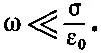(32.49)

Давайте посмотрим, какие частоты соответствуют этому приближению для такого типичного металла, как медь. Для вычисления τ воспользуемся уравнением (32.43), а для вычисления σ/ε 0— известными значениями σ и ε 0. Справочник дает нам такие данные:

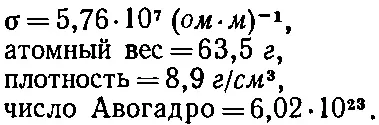
Если мы предположим, что на каждый атом приходится по одному свободному электрону, то число электронов в кубическом метре будет равно

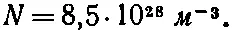
Используя далее

получаем

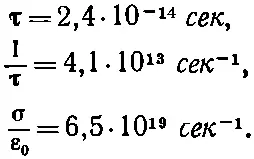
Таким образом, для частот, меньших чем приблизительно 10 12 гц , медь будет иметь описанное нами «низкочастотное» поведение. (Это будут волны с длиной, большей 0,3 мм , т. е. очень короткие радиоволны!)

Для таких волн глубина скин-слоя равна

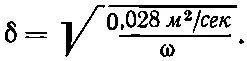
Для микроволн с частотой 10 000 Мгц (3-сантиметровые волны)

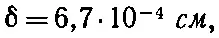
т. е. волны проникают на очень малое расстояние.

Теперь вы видите, почему при изучении полостей (и волноводов) нам нужно беспокоиться только о полях внутри полости, а не о волнах в металле или вне полости. Кроме того, мы видим, почему серебрение или золочение полости уменьшает потери в ней. Ведь потери происходят благодаря токам, которые ощутимы только в тонком слое, равном глубине скин-слоя.

Рассмотрим теперь показатель преломления в металле типа меди при высоких частотах. Для очень высоких частот ωτ много больше единицы, и уравнение (32.42) очень хорошо аппроксимируется следующим:

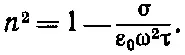(32.50)

Для высокочастотных волн показатель преломления в металлах становится чисто вещественным и меньшим единицы! Это следует также из выражения (32.38), если пренебречь диссипативным членом с γ, что может быть сделано при очень больших значениях ω. Выражение (32.38) дает при этом

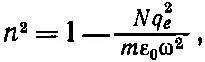(32.51)

что, разумеется, эквивалентно уравнению (32.50). Раньше нам уже встречалась величина ( Nq e 2/ε 0 m ) 1/2, которую мы назвали плазменной частотой (см. гл. 7, § 3, вып. 5):

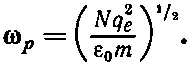
Таким образом, (32.50) или (32.51) можно переписать в виде

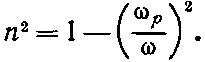
Эта плазменная частота является своего рода «критической».