Ричард Фейнман - Том 2. Электромагнетизм и материя

Фиг. 31.8. Разложение на компоненты силы F n , действующей на грани N (с единичной нормалью n) .

(Это, конечно, частный случай, но он достаточно хорошо иллюстрирует общий метод.) Дальше, напряжения, действующие на эту призмочку, должны быть такими, чтобы она находилась в равновесии (по крайней мере в пределе бесконечно малого размера), так что действующая на нее полная сила должна быть равна нулю. Силы, действующие на грани, параллельные осям координат, известны нам непосредственно из тензора S ij . А их векторная сумма должна равняться силе, действующей на грань N , так что эту силу можно выразить через S ij .

Наше допущение, что поверхностные силы, действующие на малый объем, находятся в равновесии, предполагает отсутствие объемных сил, подобных силе тяжести или псевдосилам, которые тоже могут присутствовать, если наша система координат не инерциальна. Заметьте, однако, что такие объемные силы будут пропорциональны объему призмочки и поэтому пропорциональны Δx,Δy, Δz, тогда как поверхностные силы пропорциональны ΔxΔy, ΔyΔz и т. п. Итак, если размер призмочки взять достаточно малым, то объемные силы будут пренебрежимо малы по сравнению с поверхностными.

А теперь сложим силы, действующие на нашу призмочку. Возьмемся сначала за х-компоненту, которая состоит из пяти частей, по одной от каждой грани. Но если Δz достаточно мало, то силы от треугольных граней (перпендикулярные оси z) будут равны друг другу и противоположны по направлению, поэтому о них можно забыть. На основание призмы действует x-компонента силы, равная

а x-компонента силы, действующей на вертикальную прямоугольную грань, равна

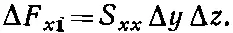
Сумма этих двух сил должна быть равна x-компоненте силы, действующей извне на грань N . Обозначим через n единичный вектор нормали к грани N , а через Δ F n— действующую на нее силу, тогда получим

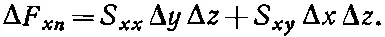
Составляющая напряжения по оси х ( S xn ), действующего в этой плоскости, равна силе ΔF xn , деленной на площадь, т. е. Δz√(Δx 2+Δy 2), или

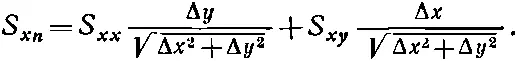
Но, как видно из фиг. 31.8, отношение Δ х /√(Δ x 2+Δy 2) — это косинус угла θ между n и осью у и может быть записан как n у , т. е. y-компонента вектора n. Аналогично, Δy/√(Δx 2+Δy 2) равно sinθ= n х . Поэтому мы можем написать

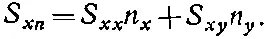
Если теперь обобщить это на произвольный элемент поверхности, то мы получим

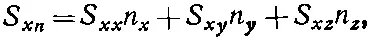
или в еще более общей форме:

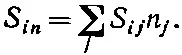(31.24)

Так что мы действительно можем выразить силу, действующую на произвольную площадь, через элементы S ij и полностью описать внутреннее напряжение.

Уравнение (31.24) говорит, что тензор S ijсвязывает силу S nс единичным вектором nточно так же, как α ijсвязывает Рс Е. Но поскольку nи S n— векторы, то компоненты S ij при изменении осей координат должны преобразовываться как тензор. Так что S ij действительно тензор.

Можно также доказать, что S ij симметричный тензор. Для этого нужно обратить внимание на силы действующие на маленький кубик в материале. Возьмем кубик, грани которого параллельны осям координат, и посмотрим на его разрез (фиг. 31.9).

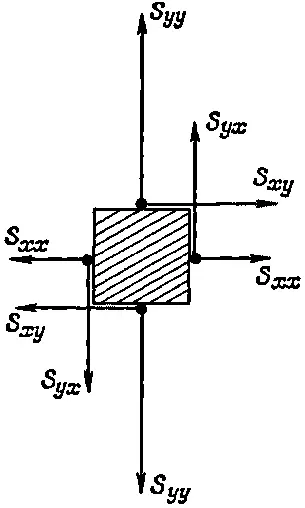
Фиг. 31.9. х- и у-компоненты сил, действующих на четыре грани маленького единичного кубика.

Если допустить что ребра куба равны единице, то х - и y -компоненты сил на гранях, перпендикулярных к осям х и у , должны быть такими, как показано на рисунке. Если взять достаточно маленький кубик, можно надеяться, что напряжение на его противоположных гранях будет отличаться ненамного, а поэтому компоненты сил должны быть равны и противоположны, как это показано на рисунке. Заметьте теперь, что на кубик не должен действовать никакой момент сил, иначе кубик начал бы вращаться. Но полный момент относительно центра равен произведению ( S yx - S xy ) на единичную длину ребра куба, а поскольку полный момент равен нулю, то S должно быть равно S xy, и тензор напряжений, таким образом, оказывается симметричным.

Благодаря этой симметрии тензора S ij его можно тоже описывать эллипсоидом с тремя главными осями. Напряжение имеет особенно простой вид на площадках, нормальных к этим осям: оно соответствует чистому сжатию или растяжению в направлении главных осей. Вдоль этих площадок нет никаких сдвиговых сил, причем такие оси, для которых отсутствуют сдвиговые силы, можно выбрать для любого напряжения. Если эллипсоид превращается в сферу, то в любом направлении действуют только нормальные силы. Это соответствует гидростатическому давлению (положительному или отрицательному). Таким образом, для гидростатического давления тензор диагонален, причем все три компоненты его равны друг другу (фактически они просто равны давлению р ). В этом случае мы можем написать

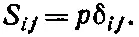(31.25)

Вообще говоря, тензор напряжений в куске твердого тела, а также его эллипсоид изменяются от точки к точке, поэтому для описания всего куска мы должны задать каждую компоненту S ij как функцию положения. Тензор напряжений, таким образом, является полем . Мы уже имели примеры скалярных полей , подобных температуре Т ( х, у , z), и векторных полей , подобных Е( х, у, z ), которые в каждой точке задавались тремя числами. А теперь перед нами пример тензорного поля , задаваемого в каждой точке пространства девятью числами, из которых для симметричного тензора S ij реально остается только шесть. Полное описание внутренних сил в произвольном твердом теле требует знания шести функций координат х, у и z.