Ричард Фейнман - Том 2. Электромагнетизм и материя

Момент инерции тела произвольной формы зависит от его ориентации относительно оси вращения. Моменты инерции прямоугольного бруска, например, относительно каждой из трех ортогональных осей будут разными. Но угловая скорость ωи момент количества движения L— оба векторы. Для вращения относительно одной из осей симметрии они параллельны. Но если моменты инерции относительно каждой из трех главных осей различны, то направления ωи L, вообще говоря, не совпадают (фиг. 31.4).

Фиг. 31.4. Момент количества движения Lтвердого предмета, вообще говоря, не параллелен вектору угловой скорости ω.

Они связаны точно таким же образом, как Еи Р, т. е. мы должны писать:

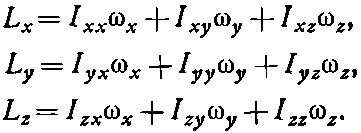(31.16)

Девять коэффициентов I ij называют тензором инерции. По аналогии с поляризацией кинетическая энергия для любого момента количества движения должна быть некоторой квадратичной формой компонент ω x, ω yи ω z:

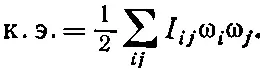(31.17)

Мы можем снова воспользоваться этим выражением для определения эллипсоида инерции. Кроме того, снова можно воспользоваться энергетическими соображениями и показать, что этот тензор симметричен, т. е. I ij = I ji .

Тензор инерции твердого тела можно написать, если известна форма тела. Нам нужно только выписать полную кинетическую энергию всех частиц тела. Частица с массой m и скоростью v обладает кинетической энергией 1/ 2 mv 2, а полная кинетическая энергия равна просто сумме

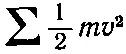
по всем частицам тела. Но скорость vкаждой частицы связана с угловой скоростью ωтвердого тела. Предположим, что тело вращается относительно центра масс, который мы будем считать покоящимся. Если при этом r— положение частицы относительно центра масс, то ее скорость vзадается выражением ω× r. Поэтому полная кинетическая энергия равна

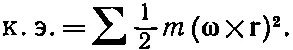(31.18)

Единственное, что нужно теперь сделать, — это переписать ω× rчерез компоненты ω х , ω y, ω zи координаты х, у, z , а затем сравнить результат с уравнением (31.17); приравнивая коэффициенты, найдем I ij . Проделывая всю эту алгебру, мы пишем:

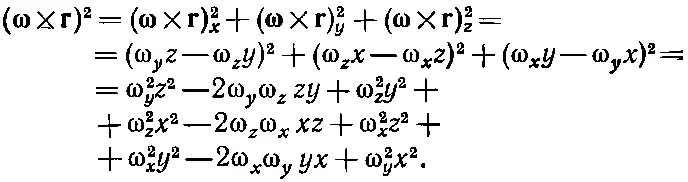
Умножая это уравнение на m/2, суммируя по всем частицам и сравнивая с уравнением (31.17), мы видим, что I xx , например, равно

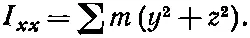
Это и есть та формула для момента инерции тела относительно оси х , которую мы получали уже раньше (гл. 19, вып. 2). Ну а поскольку r 2= x 2+ y 2+z 2, то эту же формулу можно написать в виде

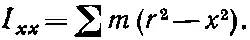
Выписав остальные члены тензора инерции, получим

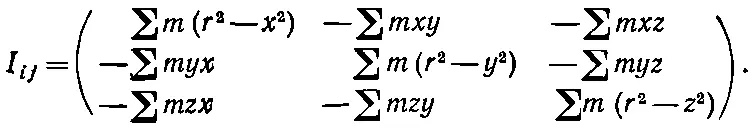(31.19)

Если хотите, его можно записать в «тензорных обозначениях»:

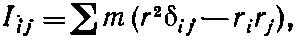(31.20)

где через r iобозначены компоненты ( х, у , z) вектора положения частицы, а ∑ означает суммирование по всем частицам. Таким образом, момент инерции есть тензор второго ранга, элементы которого определяются свойствами тела и который связывает момент количества движения Lс угловой скоростью ω:

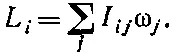(31.21)

Для любого тела независимо от его формы можно найти эллипсоид энергии, а следовательно, и три главные оси. Относительно этих осей тензор будет диагональным, так что для любого объекта всегда есть три ортогональные оси, для которых момент количества движения и угловая скорость параллельны друг другу. Они называются главными осями инерции.

Сами того не подозревая, вы пользуетесь тензором второго ранга уже начиная с гл. 20 (вып. 2). В самом деле, мы определили там «момент силы, действующий в плоскости», например τ xy, следующим образом:

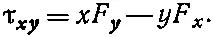
Обобщая это определение на три измерения, можно написать

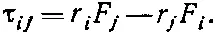(31.22)

Как видите, величина τ ij— это тензор второго ранга. Один из способов убедиться в этом — свернуть τ ijс каким-то вектором, скажем с единичным вектором е, т. е. составить

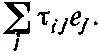
Если эта величина окажется вектором , то τ ij должен преобразовываться как тензор — это просто наше определение тензора. Подставляя выражение для τ ij, получаем

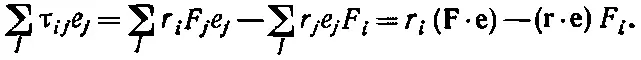
Поскольку скалярные произведения, естественно, являются скалярами, то оба слагаемых в правой части — векторы, как и их разность. Так что τ ij— действительно тензор.

Однако τ ijпринадлежит к особому сорту тензоров, он антисимметричен , т. е.

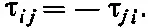
Поэтому у такого тензора есть только три разные и неравные нулю компоненты: τ xy, τ yzи τ zz. В гл. 20 (вып. 2) нам удалось показать, что эти три члена почти «по счастливой случайности» преобразуются подобно трем компонентам вектора; поэтому мы могли тогда определить вектор