Ричард Фейнман - Том 2. Электромагнетизм и материя

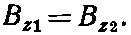(33.30)

Совершенно аналогично второе уравнение, которое дает

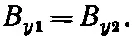(33.31)

Итак, последние три условия говорят нам, что В 2 = В 1 .

Хочу здесь подчеркнуть, что такой результат получен только потому, что по обеим сторонам границы мы взяли немагнитный материал, вернее, потому, что магнитным эффектом этих материалов мы можем пренебречь. Обычно это вполне допустимо для большинства материалов, за исключением ферромагнетиков. (Магнитные свойства материалов мы будем рассматривать в последующих главах.).

Наша программа привела нас к шести соотношениям между полями в областях 1 и 2. Все они выписаны в табл. 33.1. Их можно использовать для согласования волн в двух областях.

Таблица 33.1. граничные условия на поверхности ДИЭЛЕКТРИКА

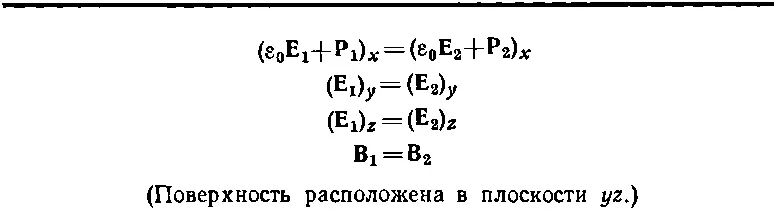
Однако я хочу отметить, что идея, которую мы только что использовали, будет работать в любой физической ситуации, где у вас есть дифференциальные уравнения и требуется найти решение в области, пересекаемой резкой границей, по обе стороны которой некоторые из физических свойств различны. Для наших теперешних целей было бы легче получить те же самые уравнения с помощью рассуждений о потоках и циркуляциях на границе. (Проверьте, можно ли подобным путем получить те же самые результаты.) Однако теперь вы знаете метод, который будет хорош, даже когда вы попали в затруднительное положение и не видите простых физических соображений относительно того, что происходит на границе. Вы можете просто воспользоваться дифференциальными уравнениями.

Теперь мы готовы применить наши граничные условия к волнам, перечисленным в § 2, где мы получили:

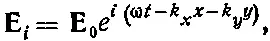(33.32)

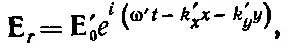(33.33)

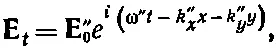(33.34)

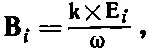(33.35)

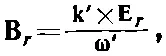(33.36)

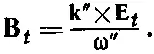(33.37)

Нами получены еще кое-какие сведения: вектор Еперпендикулярен для каждой волны вектору распространения k.

Полученный результат будет зависеть от направления вектора Е(«поляризации») в падающей волне. Анализ сильно упростится, если мы рассмотрим отдельно случай, когда вектор Е параллелен «плоскости падения» (т. е. плоскости ху ), и случай, когда он перпендикулярен к ней. Волна с любой другой поляризацией будет просто линейной комбинацией этих волн. Другими словами, отраженные и преломленные интенсивности для различных поляризаций будут разными и легче всего отобрать два простейших случая и отдельно рассмотреть их.

Я подробно проанализирую случай падающей волны, перпендикулярной к плоскости падения, а потом просто опишу вам, что получается в других случаях. Я немного жульничаю, рассматривая простейший пример, однако в обоих случаях принцип один и тот же. Итак, мы считаем, что вектор Е iимеет только z-компоненту, а поскольку все векторы Есмотрят в одном и том же направлении, векторный значок можно опустить.

Оба материала изотропны, поэтому вынужденные колебания зарядов в материале будут происходить в направлении оси z и у полей Ев преломленной и отраженной волнах тоже будет только одна z-компонента. Таким образом, для всех волн Е х и Е y , Р х и Р y равны нулю. Направления векторов Еи Вв этих волнах показаны на фиг. 33.6.

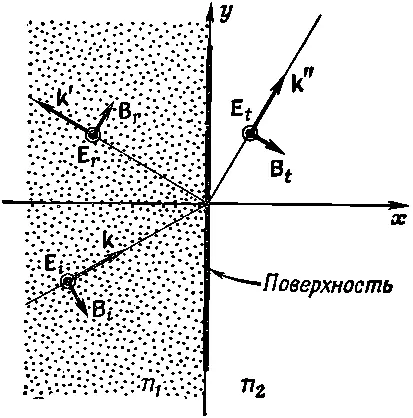
Фиг. 33.6. Поляризации отраженной и преломленной волн, когда поле Е в падающей волне перпендикулярно к плоскости падения.

(Здесь мы изменили нашему первоначальному намерению все получить из уравнений. Этот результат также можно было бы получить из граничных условий, однако, используя физические аргументы, мы избежали больших алгебраических выкладок. Когда у вас будет свободное время, посмотрите, можно ли его действительно вывести из уравнений. Он, разумеется, согласуется с уравнениями; просто мы не доказали, что отсутствуют другие возможности.)

Теперь наши граничные условия [уравнения (33.26) — (33.31)] должны дать соотношения между компонентами Еи Вв областях 1 и 2. В области 2 у нас есть только одна преломленная волна, а вот в области 1 — их две . Какую же из них нам взять? Поля в области 1 будут, разумеется, суперпозицией полей падающей и отраженной волн. (Поскольку каждое удовлетворяет уравнениям Максвелла, то им удовлетворяет и сумма.) Поэтому, когда мы используем граничные условия, нужно помнить, что

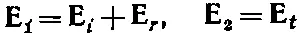
и аналогично для В.

Для поляризаций, которыми мы сейчас занимаемся, уравнения (33.26) и (33.28) не дают никакой новой информации, и только уравнение (33.27) поможет нам. Оно говорит, что на границе, т . е. при х =0:

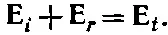
Таким образом, мы получаем уравнение

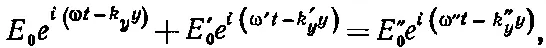(33.38)

которое должно выполняться для любого t и любого у . Возьмем сначала y=0. Для этого значения уравнение (33.38) превращается в

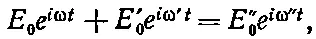
согласно которому два осциллирующих члена равны третьему. Это может произойти, только когда частоты всех осцилляции одинаковы. (Невозможно, сложив три или какое-то другое число подобных членов с различными частотами, получить для любого момента времени в результате нуль.) Итак,