Ричард Фейнман - Том 2. Электромагнетизм и материя

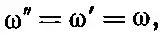(33.39)

как это и было нам всегда известно, т. е. частоты преломленной и отраженной волн те же самые, что и падающей.

Если бы мы предположили это с самого начала, то несомненно избежали бы многих трудностей, но мне хотелось показать вам, что тот же самый результат можно получить и из уравнений. А вот когда перед вами будет стоять реальная задача, лучше всего пускать в оборот сразу все, что вы знаете. Это избавит вас от лишних хлопот.

По определению абсолютная величина k задается равенством k 2=n 2ω 2/с 2, поэтому

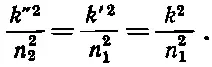(33.40)

А теперь обратимся к уравнению (33.38) для t =0. Используя снова те же рассуждения, что и прежде, но на сей раз основываясь на том, что уравнения должны быть справедливы при всех значениях у , мы получаем

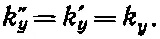(33.41)

Из формулы (33.40) k' 2=k 2, так что

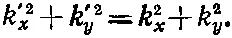
Комбинируя это с (33.41), находим

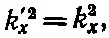
или k ' x =± k x . Знак плюс не имеет никакого смысла; он не дает нам никакой отраженной волны, а лишь другую падающую волну, и с самого начала мы говорили, что будем решать задачу с единственной падающей волной, так что

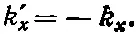(33.42)

Два соотношения (33.41) и (33.42) говорят нам, что угол отражения равен углу падения, как это и ожидалось (см. фиг. 33.3). Итак, в отраженной волне

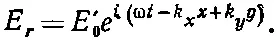(33.43)

Для преломленной волны мы уже получали

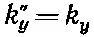
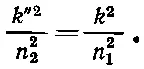(33.44)

Их можно решить и в результате получить

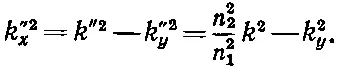(33.45)

Предположим на мгновение, что n 1и n 2— вещественные числа (т. е. что мнимая часть показателей очень мала). Тогда все k тоже будут вещественными и из фиг. 33.3 мы видим, что

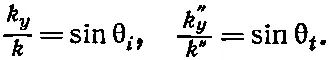(33.46)

Но ввиду уравнения (33.44) мы получаем

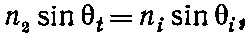(33.47)

т. е. уже известный нам закон Снелла для преломления. Если же показатель преломления не вещественный, то волновые числа оказываются комплексными и нам следует воспользоваться (33.45). [Конечно, мы могли бы определить углы θ i. и θ tиз (33.46), и тогда закон Снелла (33.47) был бы верен и в общем случае. Однако при этом углы тоже стали бы комплексными числами и, следовательно, потеряли бы свою геометрическую интерпретацию как углы. Уж лучше описывать поведение волн соответствующими комплексными величинами k xили k " x .]

До сих пор мы не обнаружили ничего нового. Мы доставили себе только простенькое развлечение, выводя очевидные вещи из сложного математического механизма. А сейчас мы готовы найти амплитуды волн, которые нам еще не известны. Используя результаты для всех ω и k , мы можем сократить экспоненциальный множитель в (33.38) и получить

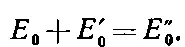(33.48)

Но поскольку мы не знаем ни Е ' 0, ни Е " 0, то необходимо еще одно соотношение. Нужно использовать еще одно граничное условие. Уравнения для Е х и Е y не помогут, ибо все Еимеют только одну z -компоненту. Так что мы должны воспользоваться условием на В. Попробуем взять (33.29):

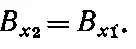
Согласно условиям (33.35)—(33.37),

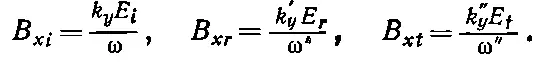
Вспоминая, что ω"=ω'=ω и k " y = k ' y = k y , получаем

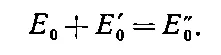
Но это снова уравнение (33.48)! Мы напрасно потратили время и получили то, что уже давно нам известно.

Можно было бы обратиться к (33.30) B z 2= В z 1, но у вектора Вотсутствует z -компонента! Осталось только одно условие — (33.31) В у 2= В у 1. Для наших трех волн

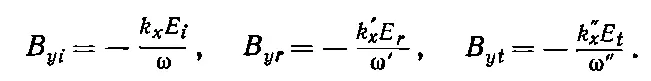(33.49)

Подставляя вместо E i , E r и E t волновые выражения при x=0 (ибо дело происходит на границе), мы получаем следующее граничное условие:

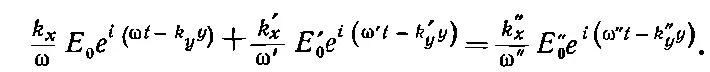
Учитывая равенство всех ω и k y , снова приходим к условию

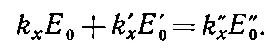(33.50)

Это дает нам уравнение для величины Е , отличное от (33.48). Получившиеся два уравнения можно решить относительно E ' 0и Е " 0. Вспоминая, что k ' x=- k x , получаем

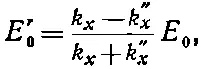(33.51)

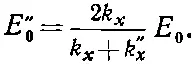(33.52)

Вместе с (33.45) или (33.46) для k " x эти формулы дают нам все, что мы хотели узнать. Следствия полученного результата мы обсудим в следующем параграфе.

Если взять поляризованную волну с вектором Е, параллельным плоскости падения, то Е, как это видно из фиг. 33.7, будет иметь как x-, так и y-компоненту.

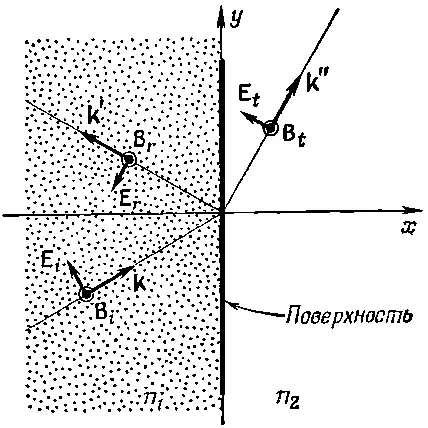
Фиг. 33.7. Поляризации волн, когда поле Ев падающей волне параллельно плоскости падения.